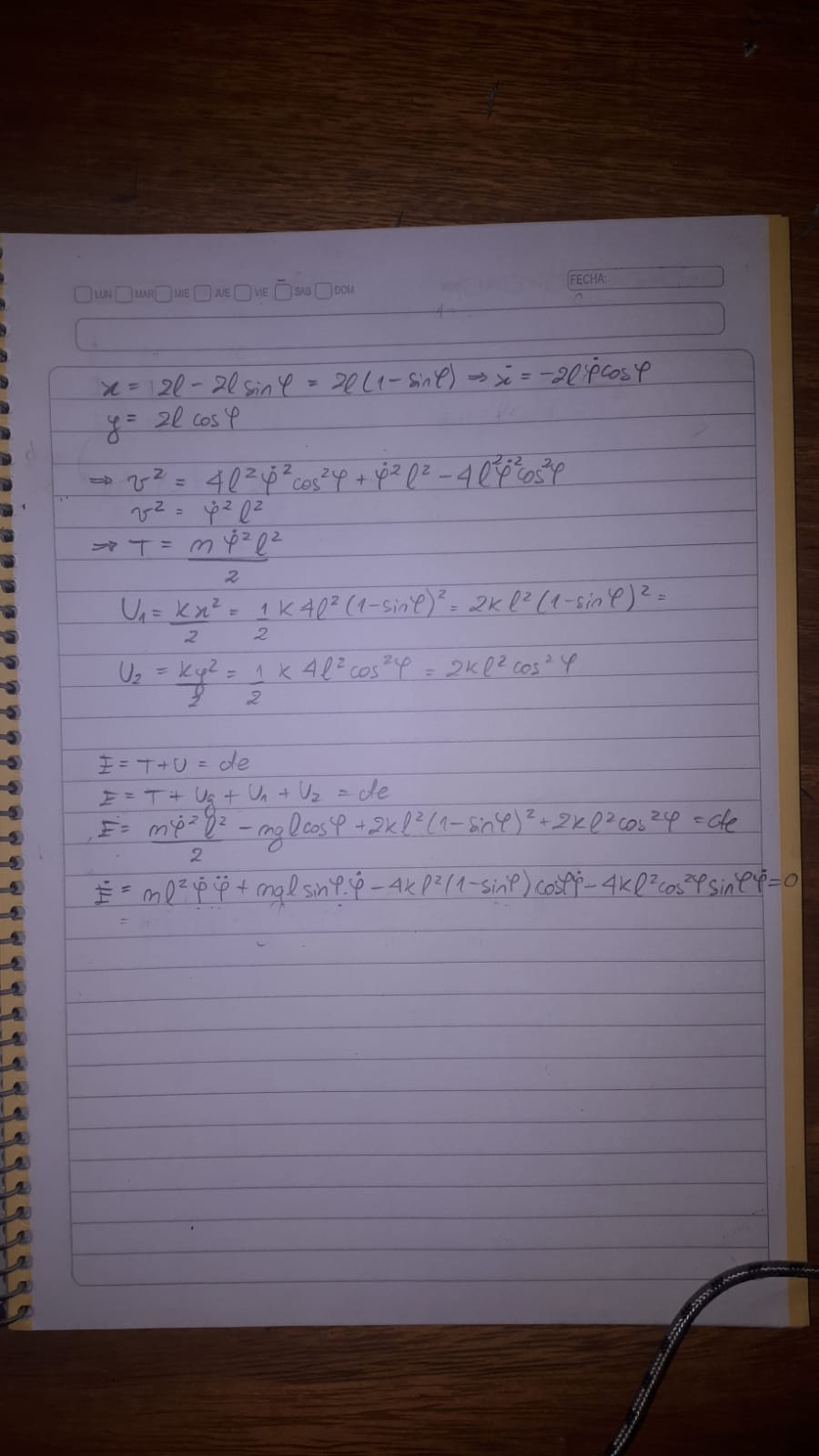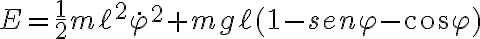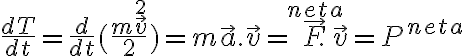Buenas, estoy teniendo problemas de cuentas con este ejercicio, adjunto la foto
Hola Silvina,
tu resultado de la energía está perfecto! Sólo te resta un poco de álgebra nomás.
Te puede simplificar un poco las cuentas desarrollar el término de energía potencial elástica del resorte horizontal que te va a permitir agrupar una parte de la misma con la energía potencial del resorte vertical, llegando a:
donde usé la constante elástica dada en la letra.
Para la ecuación de movimiento que aparece en la solución basta derivar lo anterior.
Suerte con el resto!
Ariel.
PD: La energía cinética de la partícula queda realmente muy simple, ¿no?
Hola,
Est'a bien lo que est'as haciendo. se te simplifican un poco las cosas si en la expresion para la energ'ia expandis el cuadrado y usas que sen^2 + cos^2 = 1.
Vale la pena observar que la forma tan simple de la energ'ia cin'etica se debe a que podr'ia haber calculado la velocidad de la particula tomando como origen de coordenadas el punto C, dado que este tambien es fijo en el sistema de referencia inercial. Resulta que la particula hace un movimiento circular de radio ele y angulo phi alrededor de este punto (podes convencerte de esto escribiendo el vector posicion con respecto a C en coordendas cartesianas). En virtud de esto, es claro por que queda de esa forma la energ'ia cin'etica
esero que esto te haya servido. cualquier cosa no dudes en repreguntar
g
Muchas gracias! Ya llegué a la ec de movimiento, otra duda que tengo es: yo para llegar a la ec de mov tuve que cancelar los "phi punto" de cada término y para eso tuve que asumir que era distinto de cero, pero luego para hallar las posiciones de equilibrio tengo que imponer que "phi dos puntos" es cero, ¿ahí no se usa también que "phi punto" es cero y se contradice con lo anterior?
No hay problema con simplificar el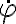 
al hallar la ecuación de movimiento, y luego hacerlo cero al hallar el equilibrio. Ese 
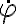que simplificaste es lo que se llama la solución introducida al demostrar el teorema de la energía. No es una solución de la ecuación de movimiento.
En efecto, el primer paso para deducir el teorema de la energía es derivar respecto al tiempo la energía cinética y luego usar la segunda ley de Newton:
donde T es la energía cinética,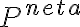 
es la potencia de la fuerza neta 
, 
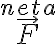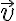la velocidad y 
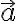la aceleración. Lo que esencialmente falta para deducir el teorema general de la energía es integrar en el tiempo esta ecuación y hacer aparecer el trabajo. Luego en un sistema conservativo el trabajo es menos la variación de la energía potencial.
O sea que básicamente al demostrar el teorema de la energía se parte de multiplicar escalarmente la segunda ley de Newton por la velocidad, y luego se integra en el tiempo. Eso es por lo que cada vez que hallemos una ecuación de movimiento derivando respecto al tiempo el teorema de la energía (paso inverso a su demostración) nos aparece la velocidad multiplicando. Que podemos simplificar, porque la pusimos allí al demostrar el teorema de la energía. En este ejercicio la velocidad es esencialmente 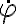, a menos de un factor multiplicativo.
Pero la ecuación de movimiento es más general que el equilibrio. Vale siempre. En particular si hay equilibrio.