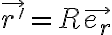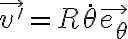Foro Práctico II

Intento responder las preguntas en el contexto del Ejercicio 13, aunque no estoy seguro de haberlas entendido del todo. 

El sistema 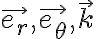$\vec{e_r}, \vec{e_ \theta } , \vec{k}$ no es inercial porque gira respecto a 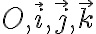$O, \vec{i}, \vec{j} , \vec{k}$, que si es inercial. Los sistemas inerciales (que son aquellos en los que vale la segunda ley de Newton) solo se trasladan con velocidad constante respecto a otro sistema inercial. Si hay un giro aparece una aceleración centrípeta, por lo tanto, el sistema está acelerado y no es inercial. Así que el sistema inercial en que vale la segunda ley de Newton es el sistema fijo $O, \vec{i}, \vec{j} , \vec{k}$. 

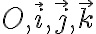Si se considera como sistema móvil o relativo el sistema 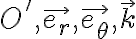 $O', \vec{e_r}, \vec{e_ \theta } , \vec{k}$, que tiene la velocidad angular que vos mencionás 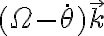$( \Omega - \dot{ \theta } ) \vec{k}$ respecto al sistema inercial 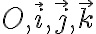$O, \vec{i}, \vec{j} , \vec{k}$, la velocidad y aceleración relativas de la partícula son 0. Esto es porque la posición relativa de la partícula respecto a  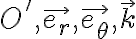$O', \vec{e_r}, \vec{e_ \theta } , \vec{k}$ es: 

$\vec{r'} = R \vec{e_r}$

y al derivarlo respecto a 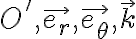 $O', \vec{e_r}, \vec{e_ \theta } , \vec{k}$, tanto R como 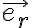$\vec{e_r}$ son fijos. Así que la velocidad absoluta de P es la velocidad de arrastre, y la aceleración absoluta es la aceleración de arrastre. 

Pero por esta razón yo creo que no es conveniente elegir ese sistema 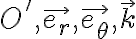 $O', \vec{e_r}, \vec{e_ \theta } , \vec{k}$ como sistema móvil o relativo en este ejercicio (porque la expresión de la aceleración de arrastre va a quedar complicada). Transformamos el problema de calcular la aceleración absoluta en uno de calcular la aceleración de arrastre. Es mejor tomar como sistema móvil un sistema intermedio que tenga como versores  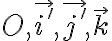$O, \vec{i'}, \vec{j'} , \vec{k}$ que se mueve con velocidad angular  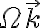 $\Omega \vec{k}$ respecto al sistema inercial  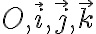$O, \vec{i}, \vec{j} , \vec{k}$ y ahí usar los teoremas de movimiento relativo en que cada componente (relativa, de arrastre o Coriolis) va a tener expresiones sencillas. Por ejemplo la velocidad relativa va a ser: 

$\vec{v'} = R \dot{ \theta } \vec{e_ \theta }$

porque ahora 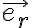$\vec{e_r}$ ya no es fijo en el sistema $O, \vec{i'}, \vec{j'} , \vec{k}$. 

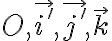Finalmente los resultados del ejercicio, tal como aparecen en la sección de resultados del práctico, no dependen de que sistema se elija como sistema móvil o relativo, porque lo que se pide es independiente de este.