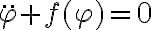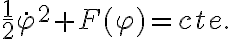Hola,
antes que nada te recomiendo que veas los Apuntes 2010, sección 3.3.1 y si querés veas la clase 11 de OpenFING para ampliar, se trata del caso del Ej 9d) pero todo lo que se ve ahí es generalizable.
Para el ejercicio 11 en concreto, si planteás la 2da ley de Newton (para lo cual necesitás la aceleración de la partícula vista desde un referencial inercial, etc) y proyectás según la dirección tangente a la guía, la ecuación de movimiento a la que llegás es de la forma:
siendo  el ángulo que te permite ubicar a la partícula sobre el aro (indicado en la figura del ejercicio).
el ángulo que te permite ubicar a la partícula sobre el aro (indicado en la figura del ejercicio).
Esta ecuación es preintegrable (multiplicás la anterior por 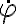 , etc.) y se llega a:
, etc.) y se llega a:
siendo 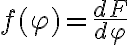 . Más allá de factores dimensionales, el primer término del lado izquierdo tiene la forma de una energía cinética (de hecho es la energía cinética relativa a la guía que te explicaba antes Ricardo) y el segundo es una función del grado de libertad
. Más allá de factores dimensionales, el primer término del lado izquierdo tiene la forma de una energía cinética (de hecho es la energía cinética relativa a la guía que te explicaba antes Ricardo) y el segundo es una función del grado de libertad  del sistema, por lo que toma en esta suerte de ecuación de conservación, el rol de una energía potencial (suma de la energía potencial de las fuerzas activas -en este caso la elástica- y el potencial de la fuerza de transporte
del sistema, por lo que toma en esta suerte de ecuación de conservación, el rol de una energía potencial (suma de la energía potencial de las fuerzas activas -en este caso la elástica- y el potencial de la fuerza de transporte 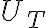 ), mientras que la constante del lado derecho representa la cantidad conservada, es decir una suerte de energía (la energía mecánica de la partícula relativa al sistema móvil). Para esta interpretación no necesitás saber las aclaraciones entre paréntesis que te hago en la frase anterior, alcanza con identificar que algo que va con el cuadrado de la derivada de la coordenada con que ubicás a la partícula es una función no nula suficiente a efectos del equilibrio y estabilidad, mientras que la función
), mientras que la constante del lado derecho representa la cantidad conservada, es decir una suerte de energía (la energía mecánica de la partícula relativa al sistema móvil). Para esta interpretación no necesitás saber las aclaraciones entre paréntesis que te hago en la frase anterior, alcanza con identificar que algo que va con el cuadrado de la derivada de la coordenada con que ubicás a la partícula es una función no nula suficiente a efectos del equilibrio y estabilidad, mientras que la función 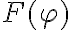 sumada a ella cumple también a efectos de equilibrio y estabilidad el rol de una energía potencial.
sumada a ella cumple también a efectos de equilibrio y estabilidad el rol de una energía potencial.
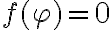 ya da las posiciones de equilibrio por ser la derivada de la función potencial y el estudio de la derivada primera de
ya da las posiciones de equilibrio por ser la derivada de la función potencial y el estudio de la derivada primera de  en las posiciones de equilibrio nos da la información acerca de la estabilidad de las mismas.
en las posiciones de equilibrio nos da la información acerca de la estabilidad de las mismas.