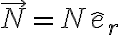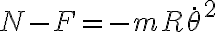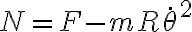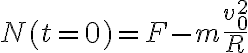En el caso del ejercicio 10, tomemos la normal como:
donde el signo de 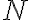 te indica si la fuerza apunta según
te indica si la fuerza apunta según 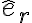 o en sentido contrario.
o en sentido contrario.
La 2da ley de Newton proyectada según la dirección radial 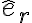 te queda:
te queda:
de donde la normal es:
Podés evaluar la expresión anterior en el instante inicial:
y de acuerdo a 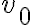 (en la letra se definen
(en la letra se definen  y
y 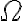 para dar una comparación) tenés un signo definido para la normal.
para dar una comparación) tenés un signo definido para la normal.
Supongamos 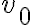 suficientemente pequeña de forma tal que
suficientemente pequeña de forma tal que  y la normal es por lo tanto iniclalmente saliente; podés suponer que este sentido de la normal se mantiene en la evolución posterior y hacer al final un test de autoconsistencia: empezás por tomar
y la normal es por lo tanto iniclalmente saliente; podés suponer que este sentido de la normal se mantiene en la evolución posterior y hacer al final un test de autoconsistencia: empezás por tomar 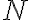 por
por 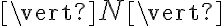 en la 2da ley de Newton proyectada según la dirección tangencial
en la 2da ley de Newton proyectada según la dirección tangencial 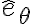 . Luego sustituís allí
. Luego sustituís allí 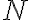 de acuerdo a Newton radial. Siguiendo un cambio de variable adecuado llegás a una ecuación diferencial de primer orden donde podés averiguar luego
de acuerdo a Newton radial. Siguiendo un cambio de variable adecuado llegás a una ecuación diferencial de primer orden donde podés averiguar luego 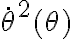 (y contestás la pregunta del ejercicio!). Con esto último podés volver a Newton según la dirección radial y verificar que efectivamente la normal mantiene el sentido saliente supuesto.
(y contestás la pregunta del ejercicio!). Con esto último podés volver a Newton según la dirección radial y verificar que efectivamente la normal mantiene el sentido saliente supuesto.
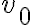 también)
también)Saludos y suerte con el ejercicio,
Ariel.