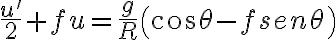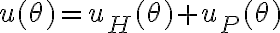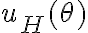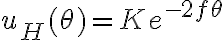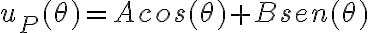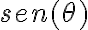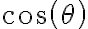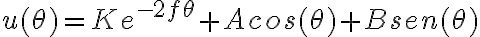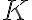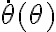MecNew: Ejercicio 9

Hola buenas noches.

Estoy intentando hacer el ejercicio 9 tal como se indicó en la pregunta anterior sobre este mismo ejercicio pero no estoy pudiendo llegar al resultado final.

El procedimiento que realice fue el siguiente:

Una vez obtenida la siguiente ecuación con el cambio de variable 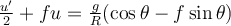$\frac{u'}{2} + f u = \frac{g}{R} (\cos\theta - f \sin\theta)$

Resolvi lo que sería la homogenea igualando a 0 lo que esta a la izquierda de la igualdad, de allí obtuve algo del estilo e´(-2f*tita) * k, el k seria la constante de la homogenea

Luego para hallar la particular supuse una solucion u(tita) = A cos(tita) + B sen(tita) y sustuti en la ecuación que está adjunta arriba el u y el u´ y despeje el A y el B despues sume ambas soluciones averiguando tambien la constante K

Por ultimo deshice el cambio de variable y despeje la velocidad.

Mi duda es si el procedimiento que realice es el correcto y tal vez tengo algun error de cuentas que no logro identificar o si tal vez tengo un error conceptual.

Gracias!

Re: Ejercicio 9

de Ariel Fernández - domingo, 12 de abril de 2020, 23:53

Hola Pablo,

tu procedimiento es correcto. Para dejarlo resumido:

partiste de la ecuación de movimiento y con un cambio de variable adecuado llegaste a:

$\frac{u'}{2}+fu=\frac{g}{R}\left(cos\theta-fsen\theta\right)$

que tiene por solución:

$u(\theta)=u_H(\theta)+u_P(\theta)$ ,

siendo $u_H(\theta)$ la solución general de la homógenea, que como bien decís es de la forma:

$u_H(\theta)=Ke^{-2f\theta}$ ,

mientras que para la solución particular $u_P(\theta)$ , tu supuesto:

$u_P(\theta)=Acos(\theta)+Bsen(\theta)$

es adecuado a que el lado derecho de tu ecuación diferencial tiene combinación de funciones $sen(\theta)$ y $cos(\theta)$

y sustituyendo $u_P(\theta)$ sos capaz de hallar las constantes $A$ y $B$ (lo que prueba que tu supuesto es válido).

Te quedó entonces una solución de la forma:

$u(\theta)=Ke^{-2f\theta}+Acos(\theta)+Bsen(\theta)$ ,

de la que resta hallar la constante $K$ , que se obtiene a partir de las condiciones iniciales (sabemos que el bloque parte del reposo en $\theta=0$ por lo que $\dot{\theta}^2(\theta=0)=u(\theta=0)=0$ ). Como bien decís también, deshaciendo el cambio de variable tenés $\dot{\theta}(\theta)$ y de allí naturalmente la velocidad en función de la posición.

Te quedan un poco de cuentas nomás, suerte!

Ariel.