Buenas, resolví el ejercicio por Newton y por energía pero no llegué al mismo resultado. No sé cuál está bien ni dónde estaría el error. Gracias
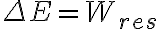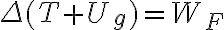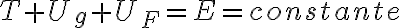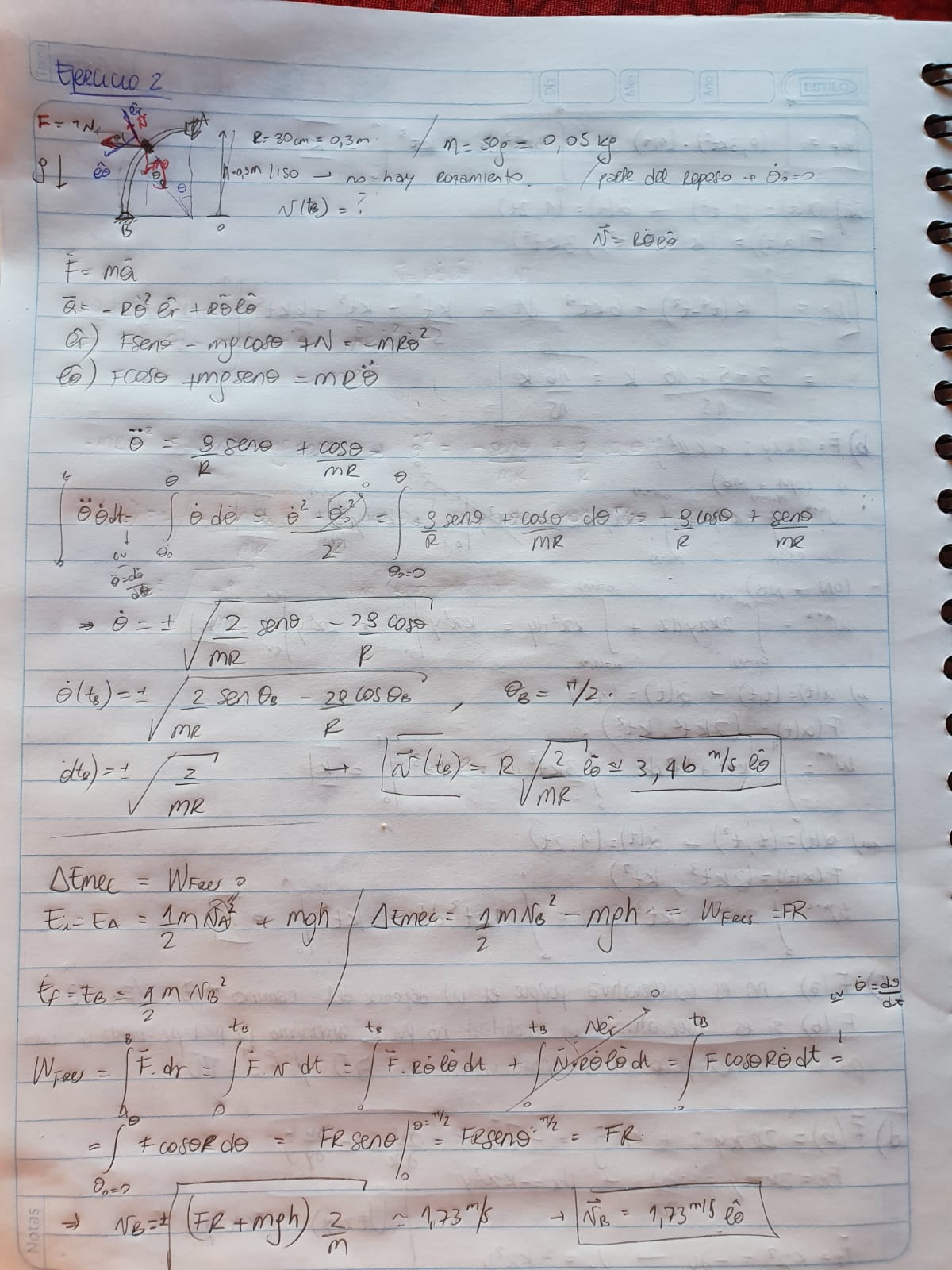
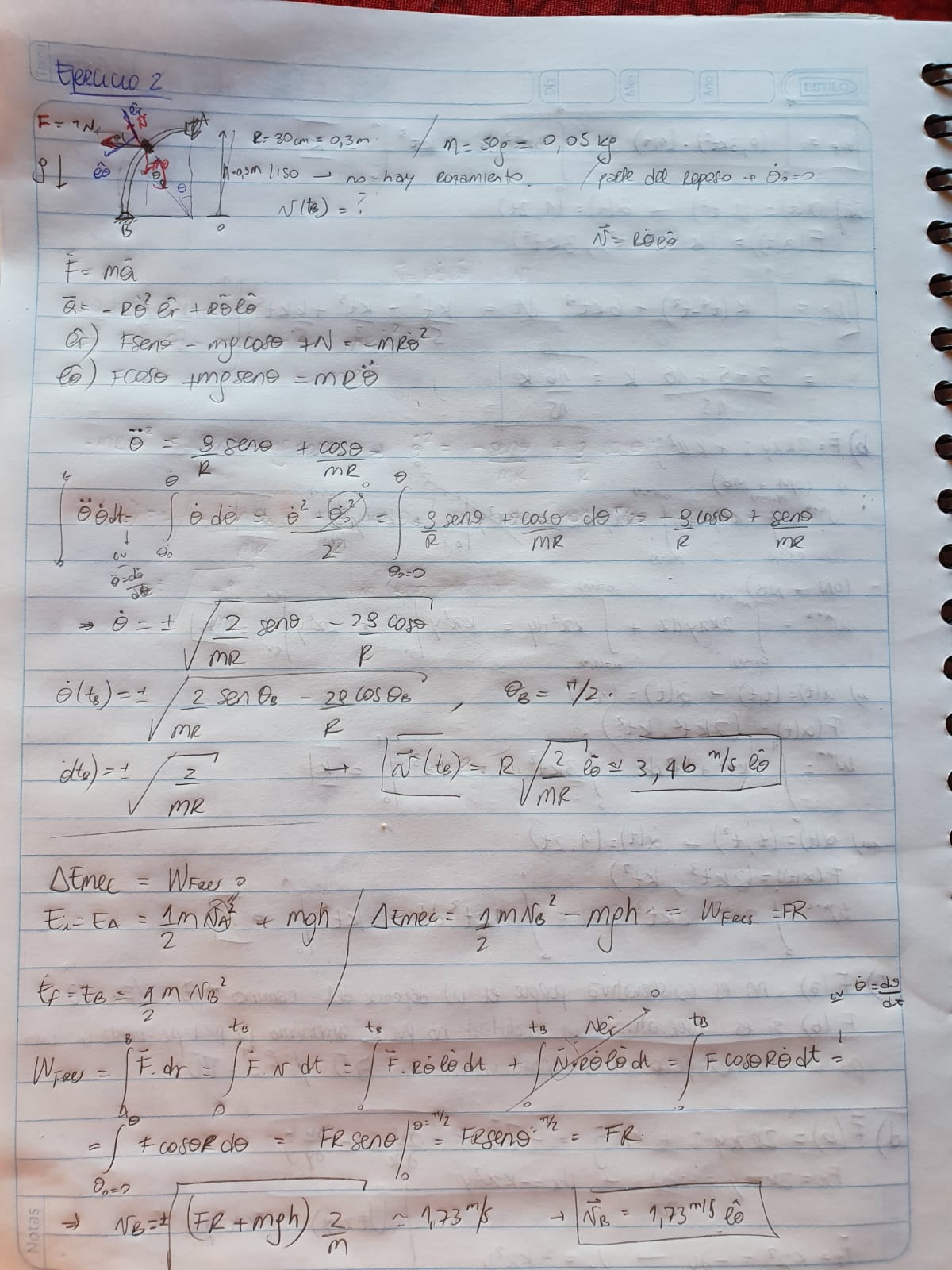
El resultado numérico al que llegué yo no coincide con ninguno de los dos resultados numéricos tuyos. Sin embargo no encuentro ningún error en tu segundo procedimiento, cuando lo hacés por la energía. Si hay un error es a la hora de sustituir los valores numéricos.
En el primer método tuyo, cuando lo hacés por Newton, al menos hay un error a la hora de preintegrar. La integral de la derecha debe ser evaluada en la posición final menos su valor en la posición inicial. Te estás olvidando que el coseno de theta no es 0 en theta igual a cero, sino que vale uno. Creo que si corregís eso te da lo mismo por los dos caminos.
Ah, claro. Muchas gracias!
Hola me surgió una duda, en la resolución del ejercicio plantea que el trabajo de la fuerza residual es el trabajo de la fuerza F, pero; ¿la fuerza F no es conservativa?.
Como sacaste que la variacion de energia mecanica es igual al trabajo de las fuerzas residuales?
Hola Marcos,
contesto también la pregunta anterior de Facundo en esta respuesta.
Si tomás de partida la Ec. (3.13) de los Apuntes 2010:
y la integrás en el tiempo, resulta:
donde la energía mecánica 
, 
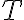es la energía cinética y 
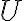la energía potencial (donde se suman las energías potenciales de todas las fuerzas conservativas que actúan sobre el sistema). En el caso de este problema 
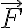es una fuerza constante en el espacio, por lo que claramente deriva de un potencial (de igual manera que la fuerza peso).
Como en el ejercicio la única fuerza que actúa sobre la partícula y no deriva de un potencial es la normal ejercida por la guía, pero la misma es de potencia nula (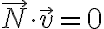
), resulta que 
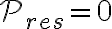y la energía se conserva (para hallar por esta vía lo pedido en el problema falta averiguar el potencial de 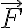, considerar el gravitatorio y despejar del balance de energía la velocidad final).
¿Qué sucede en la resolución planteada, donde en el trabajo residual se incluye el de 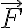?Más allá del aspecto formal mencionado antes y que estaría considerando erróneamente a la fuerza como residual, en términos de cálculo da bien, en la medida en que del lado de la energía potencial no se esté tomando en cuenta el potencial de 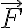también (esto duplicaría 
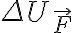o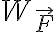 
, de la manera que lo quieran ver).
Ariel.
Muchas gracias, me quedo claro.
Saludos.
El lun., 13 de abril de 2020 22:31, Ariel Fernández (vía FING) <
Saludos.
El lun., 13 de abril de 2020 22:31, Ariel Fernández (vía FING) <
Buenas tardes, no entendí como quedaría escrita la conservación de la energía.
Al haber una única fuerza residual y la misma es de potencia nula, quedaría que la energía se conserva, en que lugar entraría luego el trabajo de la fuerza F?
La fuerza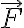 
puede considerarse a través de su trabajo en una expresión del teorema general de la energía que sería:
donde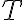 
es la energía cinética, 
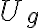la energía potencial gravitatoria y 
es el trabajo de 
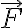. Esto valdría cualquiera sea la fuerza .
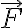Pero, una vez que se observa que 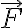también es conservativa (es una fuerza parecida al peso pero horizontal), entonces el sistema es conservativo (porque dos de las fuerzas aplicadas son conservativas y la tercera, que es la reacción es de potencia nula) y se conserva la energía mecánica total:
donde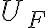 
es la energía potencial de la fuerza 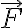que hay que hallar. Obviamente, por definición de energía potencial de una fuerza conservativa, se verifica que: 
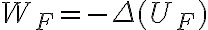y ambas expresiones son iguales.
Los dos caminos son completamente equivalentes. Lo que no hay que hacer es considerar dos veces el mismo término, y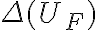 
; que aparece una sola vez a un lado u otro de la igualdad (si paso el trabajo para el otro lado de la igualdad le cambia el signo y queda 
).
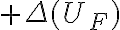Respondiendo en forma breve a tu pregunta: una vez que vemos que el sistema es conservativo, el trabajo de la fuerza 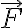aparece cambiado de signo del otro lado de la igualdad como su energía potencial (o la variación de ella).
Excelente muchas gracias!
Puede ser que igual el resultado que calculaste para el trabajo de las residuales, sea el mismo que para la energía potencial de F?.
Es decir a pesar de que no existen fuerzas residuales, cuando realizaste la integral terminaste calculando el verdadero trabajo de la fuerza conservativa F. Cuando hice el cálculo de la energía potencial asociada a F me dio eso Ufuerza F=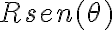
y me gustaría corroborar si está bien.
Puede ser que igual el resultado que calculaste para el trabajo de las residuales, sea el mismo que para la energía potencial de F?.
Es decir a pesar de que no existen fuerzas residuales, cuando realizaste la integral terminaste calculando el verdadero trabajo de la fuerza conservativa F. Cuando hice el cálculo de la energía potencial asociada a F me dio eso Ufuerza F=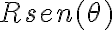 y me gustaría corroborar si está bien.
Nahuel, que tal?
No estoy seguro de entender bien tu pregunta, pero como explicaron arriba mis colegas, la fuerza F es conservativa, aunque, si uno no se da cuenta de ello y prosigue a calcular el trabajo de la misma como fuerza residual, el resultado termina siendo el mismo que al calcular el potencial del cual deriva la fuerza, como explicaron Ricardo y Ariel.
De todas formas, el potencial al que llegaste está bien. Solo te queda plantear la conservación de la energía con esos dos potenciales y despejar la velocidad final. Sin embargo, te aconsejaría trabajar en cartesianas, ya que, tanto el peso, como la fuerza F, son más fáciles de expresar en cartesianas. Pero como vos prefieras! El resultado va a ser el mismo.
Cualquier cosa no dudes en preguntar!
Tomás
Perfecto quedó resuelto, muchas gracias!
El vie., 17 abr. 2020 14:01, Juan Tomas Urruzola Abdala (vía FING) <
El vie., 17 abr. 2020 14:01, Juan Tomas Urruzola Abdala (vía FING) <