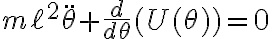Hola Vanessa,
tu pregunta tiene varias partes, voy contestando de acuerdo a como tenés desarrollado el problema y está en las imágenes:
i) el factor de 4 que te sobra proviene de que el vector posición de la masa 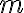 no está bien escrito y debería cumplir:
no está bien escrito y debería cumplir:
con lo que al derivar hallás la velocidad correcta y de ahí en más el ejercicio va a ir bien.
ii) La energía del sistema es:
y usando que esta cantidad se conserva en el tiempo (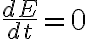 ) podemos derivar
) podemos derivar 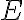 :
:
y obtener de allí la ecuación de movimiento (ojo de aquí en más porque ví en tu desarrollo que considerás la derivada de la energía cinética respecto de  y de
y de 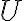 con respecto a
con respecto a  , vamos a ver cómo derivar correctamente).
Derivemos entonces la energía:
, vamos a ver cómo derivar correctamente).
Derivemos entonces la energía:
en cada término usamos la regla de la cadena adecuadamente:
donde el segundo término del producto del lado derecho es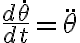 :
:
Para el siguiente término procedemos análogamente:
con lo que juntando los dos términos te queda:
o lo que es lo mismo:
siendo lo que multiplica a la ecuación de movimiento (
la ecuación de movimiento (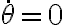 es una solución trivial que dice que la energía no varía si el sistema no se mueve nunca
y además viene desde el paso cero del planteo energético a partir de Newton):
es una solución trivial que dice que la energía no varía si el sistema no se mueve nunca
y además viene desde el paso cero del planteo energético a partir de Newton):
Hasta ahí las derivadas temporales que deberías revisar. Al llegar a la ecuación de movimiento fijate que las posiciones de equilibrio (correspondientes a todas las derivadas temporales nulas, es decir en este caso 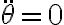 ) se dan para
) se dan para 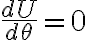 ,
y allí conectamos con tus preguntas acerca de la energía potencial:
,
y allí conectamos con tus preguntas acerca de la energía potencial:
iii) los puntos de equilibrio, en sistemas donde se conserva la energía (o no conservativos preintegrables) son aquellos donde la energía potencial (o potencial eficaz) tiene extremos relativos:
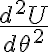 alrededor de la posición de equilibrio y si esta derivada segunda es no nula, inferir de qué tipo de extremo se trata; si fuera nula, se aplican otras
herramientas de análisis o se ven derivadas de mayor orden).
alrededor de la posición de equilibrio y si esta derivada segunda es no nula, inferir de qué tipo de extremo se trata; si fuera nula, se aplican otras
herramientas de análisis o se ven derivadas de mayor orden).No sé si pude capturar todas tus dudas, cualquier cosa volvé a preguntar nomás.
Saludos,
Ariel.

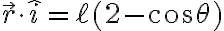
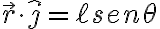
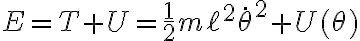
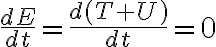
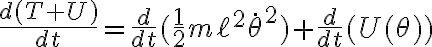
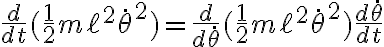
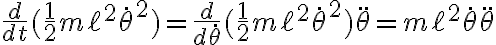
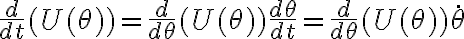
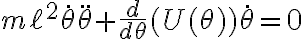
![[m\ell^2\ddot{\theta}+\frac{d}{d\theta}(U(\theta))]\dot{\theta}=0 [m\ell^2\ddot{\theta}+\frac{d}{d\theta}(U(\theta))]\dot{\theta}=0](https://eva.fing.edu.uy/filter/tex/pix.php/c5d77697fb50ae9918f0c4d510fdcdb8.gif)