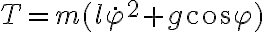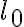Foro Práctico II

$l_0$ es la longitud del hilo cuando 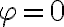$\varphi=0$, y depende de cuánto hilo se ha desenrollado hasta ese ángulo. Si la partícula arranca en 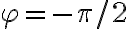$\varphi= -\pi/2$ (el extremo izquiero del disco), al llegar a 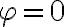$\varphi= 0$ se va a haber desenrollado más hilo que si esta arrancaba en 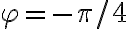$\varphi= -\pi/4$ por ejemplo. 

Luego, con respecto a la pregunta d), la tensión te debería haber quedado algo así:

$T= m (l \dot{\varphi}^2 + g \cos\varphi)$

En el intervalo 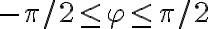$-\pi / 2 \leq \varphi \leq \pi / 2$ coseno es siempre mayor o igual a cero por lo que la tensión va a ser siempre mayor o igual a cero también, el hilo va a estar siempre tenso. Si el ángulo inicial es menor a 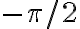$-\pi/ 2$ (la partícula empieza pegada al disco por encima de su "ecuador"), al empezar a caer el hilo podría "arrugarse". Fijate que en ese caso el segundo sumando en la tensión es negativo por lo que para que el hilo no se arrugue le tengo que dar una velocidad inicial lo suficientemente grande. En el caso de este ejercicio la condición inicial es velocidad inicial nula por lo que si el hilo se enrolla más allá de 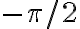$-\pi/ 2$ ya desde el instante inicial no va a estar tenso.

Edito: En mi respuesta anterior al final había dicho producto escalar pero era vectorial.