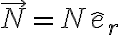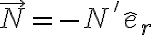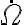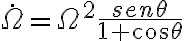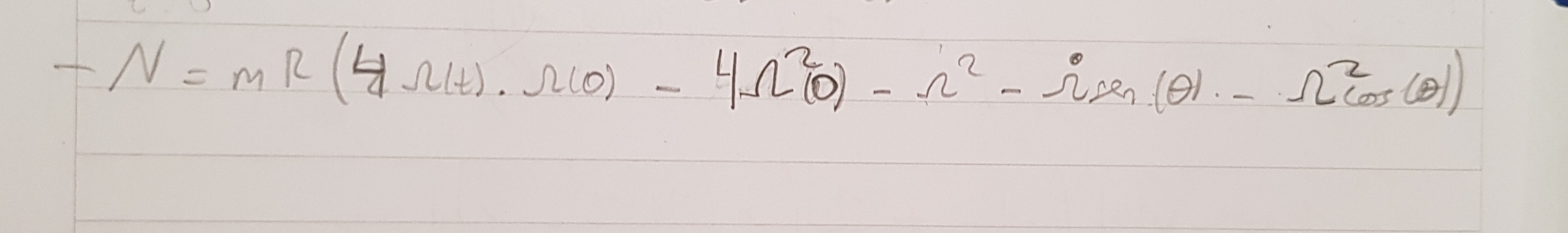
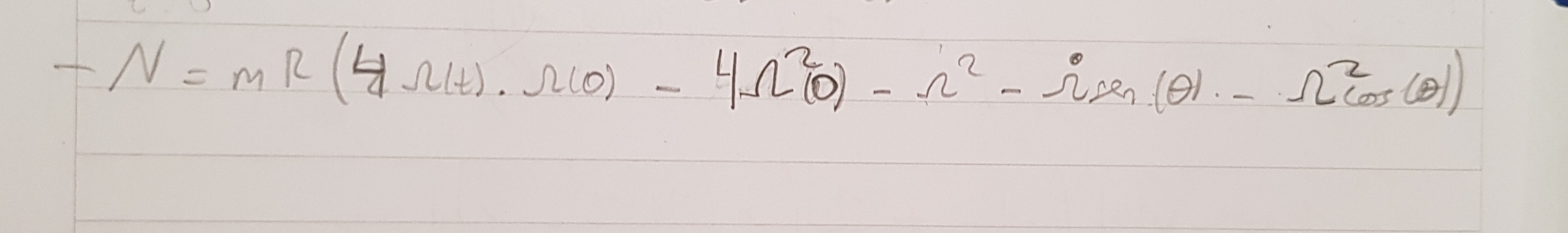
Hola,
El signo negativo global no es a priori un problema ya que el vínculo es bilateral, la reacción normal no tiene por qué apuntar en principio en un sentido dado para asegurar el movimiento de la partícula según el vínculo: llamale 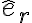 al versor que va del centro de la circunferencia a la partícula, con lo cual podrías escribir en forma estándar la reacción normal como
al versor que va del centro de la circunferencia a la partícula, con lo cual podrías escribir en forma estándar la reacción normal como
esta función 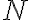 es la expresada en el resultado del ejercicio, pero si vos hubieras definido tu reacción (llamémosle
es la expresada en el resultado del ejercicio, pero si vos hubieras definido tu reacción (llamémosle 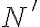 para diferenciar) con el signo opuesto:
para diferenciar) con el signo opuesto:
no habría problema porque 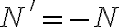 hace compatible los dos resultados.
hace compatible los dos resultados.
 , pero de todas formas para llegar al resultado final vas a tener que sustituir
, pero de todas formas para llegar al resultado final vas a tener que sustituir 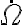 en términos de
en términos de 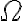 y
y  , lo que ya tenés a partir de la ecuación diferencial de partida que te permitió averiguar
, lo que ya tenés a partir de la ecuación diferencial de partida que te permitió averiguar 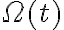 en a).
en a).Espero que te haya ayudado y cualquier cosa volvé a preguntar con un desarrollo ampliado.
Saludos,
Ariel.
Buenas, estoy en la misma situación que el compañero, independientemente de como nombre theta dicha variable me queda dependiente del tiempo(mas específicamente es una constante multiplicada por el tiempo) y no logro llegar a la solución del problema debido a que tengo un seno y un coseno de una variable que depende del tiempo, términos que no aparecen en la solución.
Desde ya gracias
Muchas gracias por tu respuesta.
Ya había intentado esto y tuve un error en la cuenta.
Ya logre llegar al resultado.
Gracias!.