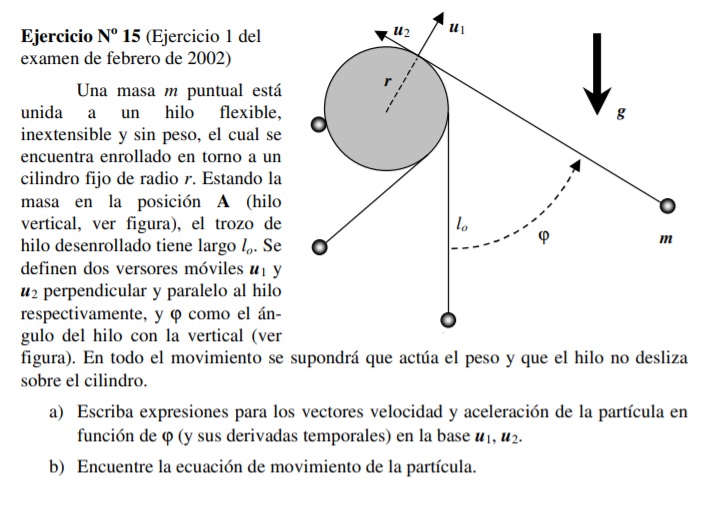
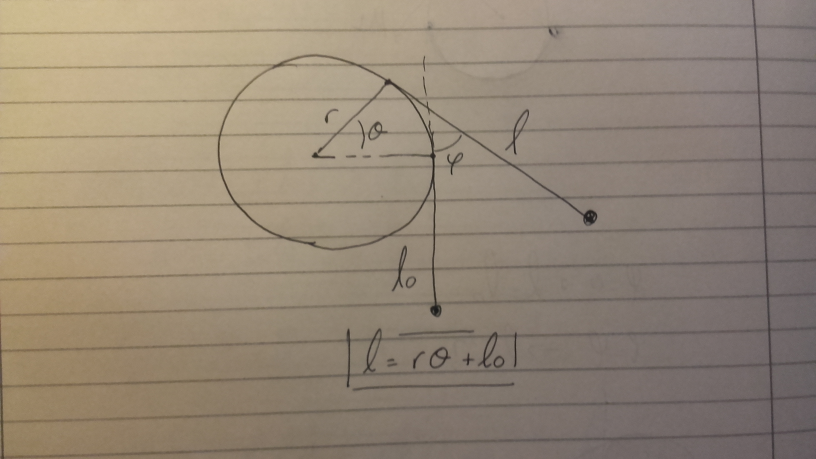
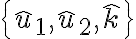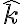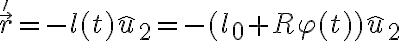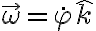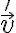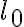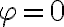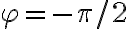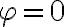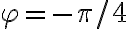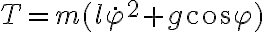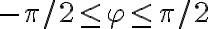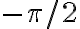Buenas, no logro encontrar una forma de plantear este ejercicio para llegar a la solución de la parte a).
No logro encontrar la forma de expresar la posición correctamente. Ya que no encuentro la manera de vincular los valores r,phi, y l0, para conseguir la posición de la partícula, que según tengo entendido varía según el ángulo phi.
Se que la posición de la partícula va a variar en función del ángulo pero no llego a expresarla usando los sistemas que propone el ejercicio.
Mas concretamente me parece que lo que no logro interpretar bien es la condición de que el hilo no desliza, ya que es la unica informacion del problema que no eh logrado tomar en cuenta.
Adjunto una foto del ejercicio.
Desde ya gracias.