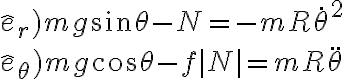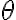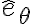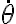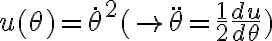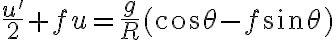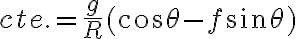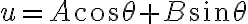Foro Práctico II

Hay que usar las dos ecuaciones sí. La normal te queda en términos de la misma velocidad angular. En este problema es conveniente escribir las ecuaciones de movimiento en coordenadas polares:

(Perdón por la iamgen rotada, por más que rote la imagen original el EVA lo deja siempre en esta orientación por alguna razón).

En los versores de la figura, las ecuaciones de Newton te quedarían:

$\hat{e}_r ) mg \sin\theta - N = - m R \dot{\theta}^2 \\ \hat{e}_\theta ) mg \cos\theta - f |N| = m R \ddot{\theta}$

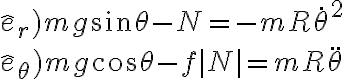
El módulo de N se puede obtener de la primer ecuación:

$|N|=mg \sin\theta + mR \dot{\theta}^2$

Observar que ambos sumandos son positivos por lo que el lado derecho es efectivamente el módulo de N ( 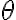$\theta$ va entre cero y $\pi / 2$ en este problema).

Al sustituir esto en la componente 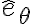$\hat{e}_\theta$ te va a quedar una ecuación diferencial para el ángulo 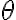$\theta$. La ecuación es no lineal (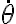$\dot{\theta}$ está elevado al cuadrado) por lo que es conveniente usar la sugerencia de la letra y hacer el cambio de variable 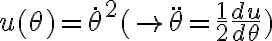$u(\theta) = \dot{\theta}^2 ~~ (\rightarrow \ddot{\theta} = \frac{1}{2} \frac{du}{d\theta})$. La ecuación entonces pasa a ser lineal y perfectamente resoluble. En vez de resolver para el ángulo en función del tiempo, vas a resolver para la velocidad angular en función de la posición, cambió la variable independiente de t a $\theta$.

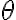Una vez resuelta la ecuación, ahí ya podés evaluar en ángulo pi/2 para responder la pregunta.