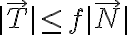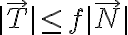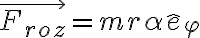Buenas, quisiera saber como se plantea este ejercicio pq no llego al resultado y creo q mi error se encuentra ahí
El equilibrio se mantiene mientras se verifique la condición de Coulomb para el rozamiento estático:
donde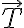 
es la reacción tangencial del vínculo y 
la componente normal de esa reacción. Como se trata de un apoyo en una superficie, la primera puede tener dos componentes y la segunda solo una.
Para hallar esas reacciones se plantea la segunda ley de Newton al bloque, donde además de esa reacción actúa el peso y las fuerzas ficticias (si nos paramos en el sistema relativo al disco).
Como suponemos que el bloque está en equilibrio relativo al disco (mientras se verifique esa condición), las aceleración y velocidad relativa son nulas. Luego la aceleración de Coriolis también será nula. Hay que calcular la aceleración de arrastre que tiene dos componentes: una debido a la aceleración angular y otra debido a la aceleración centrípeta. Proyectando Newton estas dan las dos componentes de 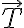, y la normal es igual al peso.
Yo tengo una duda de como imponer la condición de deslizamiento desde el comienzo (lo último que pide el ejercicio), no entiendo si tengo que imponer que la vel. angular es nula dado que apenas coloco el bloque y ya desliza o es otra cosa que estoy omitiendo. Saludos
Sí, ese es un caso, que la velocidad angular hallada antes sea nula. Pero la respuesta es más general que ese caso. Podrías pensarlo para cuando la aceleración angular es mayor que ese caso límite. Esta es una respuesta semi-intuitiva que da la respuesta correcta. Pero en esta asignatura queremos deducir los resultados analíticamente.
La respuesta formal a esa última pregunta se obtiene pensando que la respuesta a la pregunta anterior (a qué velocidad angular el bloque empieza a deslizar) no tenga solución. Fijate que si la aceleración angular es muy grande (estrictamente mayor que fg/r), la raíz cuarta que queda en la respuesta de esa pregunta, tendrá radicando negativo. O sea, que no existe un valor real para esa velocidad angular. Si habría un número complejo que la verifica, pero la respuesta tiene que ser un número real que podamos medir experimentalmente con un medidor de velocidad angular. Si la velocidad angular no es real, entonces la condición de no deslizamiento no se puede verificar nunca, y el bloque deslizará siempre (desde el comienzo). Coincide con el razonamiento anterior: que la aceleración angular sea mayor (o igual) que el caso en que la velocidad angular es nula.
Hola buenas, no logro entender cómo interpretar que si la velocidad hallada no existe (si diese un numero complejo) entonces esto significa que se desliza desde el comienzo, mi intuición al resolver el ejercicio fue que si el valor de w no existe entonces no hay una velocidad w para la cual se desprende, por ende el bloque nunca se desprende del disco. Entiendo porque para aceleraciones angulares mayores al caso w=0 tambien debe desprenderse immediatamente(de este modo llegue a la solución correcta) pero no logro llegar a la conclusion que llegaste en este comentario.
¿Porque si la velocidad angular no existe debo asumir que es porque se desprende al inicio?
¿Cual es la condición de no deslizamiento que mencionas en el comentario?
Desde ya gracias
En tu mensaje hablás de desprendimiento, y en este ejercicio el bloque no se desprende nunca (porque la normal es siempre igual a mg). Supongo que te referís al deslizamiento.
La condición de no deslizamiento es:
(ver una de mis respuestas anterior, creo que es la primera).
Si no podemos hallar una región de ω reales que verifiquen esta condición, quiere decir que la condición no se verifica nunca. Entonces el bloque desliza.
Hay dos formas de pensarlo. Una es simplemente buscar para que valores de alfa desliza en el instante inicial. En el instante inicial la velocidad angular omega es cero, por lo que en ese instante la aceleración sólo tiene componente tangencial, por lo que, usando Newton, la fuerza de rozamiento estático sólo tiene componente tangencial:
(importante: esta expresión anterior solo vale en el instante inicial)
Ahora imponemos que en ese instante deslice. Lo que tiene que suceder para que deslice es que el módulo de la fuerza de roz sea mayor o igual al módulo de la normal. De ahí se llega a que el VALOR ABSOLUTO de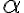 
tiene que ser mayor o igual a 
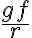. Notar que aparece el valor absoluto de 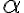por que la condición de deslizamiento es sobre módulos. Observar que la cond de deslizamiento en el instante inicial es alfa mayor o igual a cierto mínimo, lo cual es perfectamente intuitivo: si desliza desde el vamos para una aceleración, lo va a hacer para cualquier aceleración mayor.
Ahora bien, ¿cómo interpretamos esta cuestión de la raíz cuarta y omega imaginario?
Una forma de pensarlo es ver que a medida que alfa aumenta, el omega para el que desliza el bloque es cada vez menor. Si seguimos aumentando alfa, llegamos a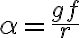 
, valor para el cual el omega de deslizamiento es cero. Ese es el valor mas chico de alfa para el cual deslizamos en el instante inicial (dado que en el instante inicial omega es cero). Para valores mas chicos de alfa el deslizamiento sucede posteriormente, dado que sucede con omega no nulo. Para valores de alfa mayores que este limite, la solucion para omega no tiene sentido: no tiene sentido omega imaginario. Pero por el razonamiento anterior, si para un valor de alfa desliza desde el inicio, también lo hará para cualquier valor mayor, más allá de que la solución hallada antes para omega no tiene sentido extenderla para este rango de alfas.
En fin, no se si esto responde o no tu pregunta. RESUMIENDO: Yo diría que no pienses en buscar omegas imaginarios, si no pensa en la condición de no-deslizamiento y para que rango de alfas esta condición se rompe ya en el instante inicial.
Si tenes mas preguntas no dudes en repreguntar.
G
Me queda claro el razonamiento y luego de investigar la condición de no deslizamiento pude entender mas o menos como se llega a la conclusión.
Gracias por las respuestas!