Gracias!!
Buenas, necesitaría alguna ayuda a la hora de de hallar la velocidad absoluta del bloque. Yo comencé con aplicar Roberval, para eso me definí un sistema fijo {er, e&, k’} con centro en A (mismo centro que el sistema movil {i’,j’,k’}). El primer término de la velocidad (velocidad relativa respecto al sistema movil) es el calculado en la parte a pero estoy teniendo problemas para calcular el termino de transporte. No se si debería plantearme otro sistema sistema fijo o mover el que planteé al centro de la esfera o comencé encarando mal el ejercicio jajaj. Cualquier ayuda me vendría bien porque estoy trancando en esto.
Hola Federico,
no podés considerar como sistema absoluto uno con centro en 
ya que este punto está acelerado (describe un movimiento circular uniforme sobre una circunferencia de radio 
). Para aplicar Roberval y Coriolis y hallar la velocidad y aceleración absolutas respectivamente, necesitás como referencial absoluto a la circunferencia (podés tomar como origen de ese sistema el centro 
de la misma).
Saludos,
Ariel.
Ahi va gracias!
Entonces me tomo un sistema fijo S en el centro de la cfa {er, e&, k’} y uno S’ solidario a la plataforma {i’,j’,l’} con centro en A? Porque a la hora de hallar la velocidad de transporte estoy teniendo problemas y no me da lo mismo que en la solución planteada en el parcial.
Disculpa la molestia.
Hola,
corregime si me equivoco porque no tengo tu esquema del ejercicio, pero por los nombres de tus versores me suena que lo que estás tomando como Sistema Absoluto 
es uno que gira acompañando al punto : ese sistema no es inercial, no podés por lo tanto plantear desde allí directamente la segunda ley de Newton; puede que eso sea lo que te esté dando problemas.
Saludos,
Ariel.
En un principio me había tomado los dos sistemas desde A luego con la corrección tuya traslade uno hacia el centro de la circunferencia llegando a:
- S'={A,i',j',k'} con centro en A solidario a la plataforma (dado por letra)
- S={O,er,eø,k'} con centro en O (centro de la cfa) fijo. Este sistema ve moverse a S'.
Pero creo que no esta bien lo que plantee porque al realizar la parte b) no logro hallar bien el termino de la velocidad de transporte. Me vendría bien una explicación sobre la elección de los sistemas en este ejercicio en particular porque hace días que me tiene trancado y no lo logro avanzar jajaj.
Lo que te respondía Ariel es que en tu sistema S parece que ponés versores móviles (si usás la misma notación que en la resolución del parcial). Entonces ese sistema no es absoluto (fijo respecto a la circunferencia). Un sistema fijo sería: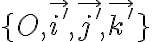 
.
Observá que en este ejercicio la plataforma solo se traslada (no gira), porque se mantiene siempre paralela a sí misma. Luego la velocidad de arrastre o transporte será la velocidad de cualquier punto de la plataforma, por ejemplo A.
Bien! Vi el video que subieron sobre la resolución de este ejercicio y logre entenderlo!
Muchas gracias!