Buenas
Me podrían dar una mano con el ejercicio 7c? No entiendo como llega a las condiciones de la solución
Gracias
Buenas
Me podrían dar una mano con el ejercicio 7c? No entiendo como llega a las condiciones de la solución
Gracias
Hola Martin,
en la parte c) de este ejercicio tenés que hallar el ángulo en que la partícula pierde contacto con la guía; si 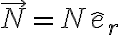 es la reacción normal ejercida por la guía (con el versor
es la reacción normal ejercida por la guía (con el versor  apuntando del centro de la guía hacia la partícula) sabés que en la medida en que la partícula esté en contacto con el exterior de la guía (es un vínculo unilateral) se debe cumplir que
apuntando del centro de la guía hacia la partícula) sabés que en la medida en que la partícula esté en contacto con el exterior de la guía (es un vínculo unilateral) se debe cumplir que 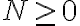 .
.
Por lo tanto, el objetivo es que halles  (vas a necesitar la proyección de la segunda ley de Newton que no usaste en a) y la velocidad en función de la posición que obtuviste en b), podés sacar alguna idea muy similar del ejercicio resuelto II.8) y analices su dependencia con
(vas a necesitar la proyección de la segunda ley de Newton que no usaste en a) y la velocidad en función de la posición que obtuviste en b), podés sacar alguna idea muy similar del ejercicio resuelto II.8) y analices su dependencia con  , ángulo que forma
, ángulo que forma 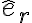 con respecto a la vertical (
con respecto a la vertical (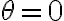 al comienzo del movimiento).
al comienzo del movimiento).
Saludos,
Ariel.
Buenas, llegue al resultado correcto de θ de desprendimiento, pero no entiendo como hallo la condicion que pusieron en la hoja de resultados "si v0≤ sqrt(gR)"
Si 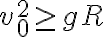 entonces el coseno queda mayor a 1 por lo que el ángulo no existe. Si se cumple esta condición podés además observar que si evaluas la normal en cero te queda negativa ya desde el principio, por lo que la partícula se desprendería ya en el instante inicial.
entonces el coseno queda mayor a 1 por lo que el ángulo no existe. Si se cumple esta condición podés además observar que si evaluas la normal en cero te queda negativa ya desde el principio, por lo que la partícula se desprendería ya en el instante inicial.
muchas gracias!
No entiendo por qué si (vo)^2 > gR entonces la masa se desprende inicialmente. Yo cuando impongo que (vo)^2 > gR obtengo que el coseno del ángulo de desprendimiento es mayor a 1 pero el coseno de un ángulo nunca podría ser mayor a 1, cuál es la interpretación de eso?
Que el coseno del ángulo te de mayor que uno, implica que no existe ningún ángulo que verifique la condición N ≥ 0, necesaria para que el vínculo se mantenga. Entonces la condición no se verifica nunca, y la partícula desprende desde el instante inicial.
La interpretación, como dice Esteban, es que la normal en el instante inicial te daría negativa, lo que implica que en ese instante la partícula ya está desprendiendo.
Más explícitamente la normal te debería dar:
donde R es el radio de la guía, y N es la componente saliente de la normal, que debe ser positiva (o nula) para que se mantenga el vínculo. Si 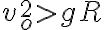 , N < 0 para todo
, N < 0 para todo 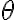 , incluso
, incluso 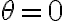 (que es cuando el coseno es más grande). Ese ángulo
(que es cuando el coseno es más grande). Ese ángulo 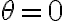 coincide con la posición inicial. O sea que inicialmente el vínculo no se puede mantener, y la partícula se desprende de la guía ya en el instante inicial.
coincide con la posición inicial. O sea que inicialmente el vínculo no se puede mantener, y la partícula se desprende de la guía ya en el instante inicial.
De hecho la partícula, al estar desprendida va a seguir un movimiento de proyectil (movimiento parabólico). La parábola va a ser tangente a la circunferencia en la posición inicial. Se puede demostrar que el radio de curvatura de la parábola en el instante inicial es 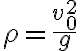 . Si ρ > R, la partícula sigue la ley de proyectil y se desprende. Si ρ < R, la parábola penetraría la circunferencia, entonces la partícula queda vinculada a la guía circular.
. Si ρ > R, la partícula sigue la ley de proyectil y se desprende. Si ρ < R, la parábola penetraría la circunferencia, entonces la partícula queda vinculada a la guía circular.
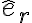 y el resultado de la preintegración de la 2da ley según
y el resultado de la preintegración de la 2da ley según 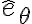 tenés lo necesario para hallar la normal y después tenes que analizar el resultado y que pasa según
tenés lo necesario para hallar la normal y después tenes que analizar el resultado y que pasa según 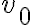 .
.