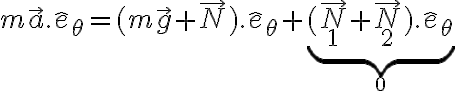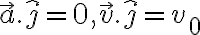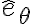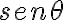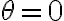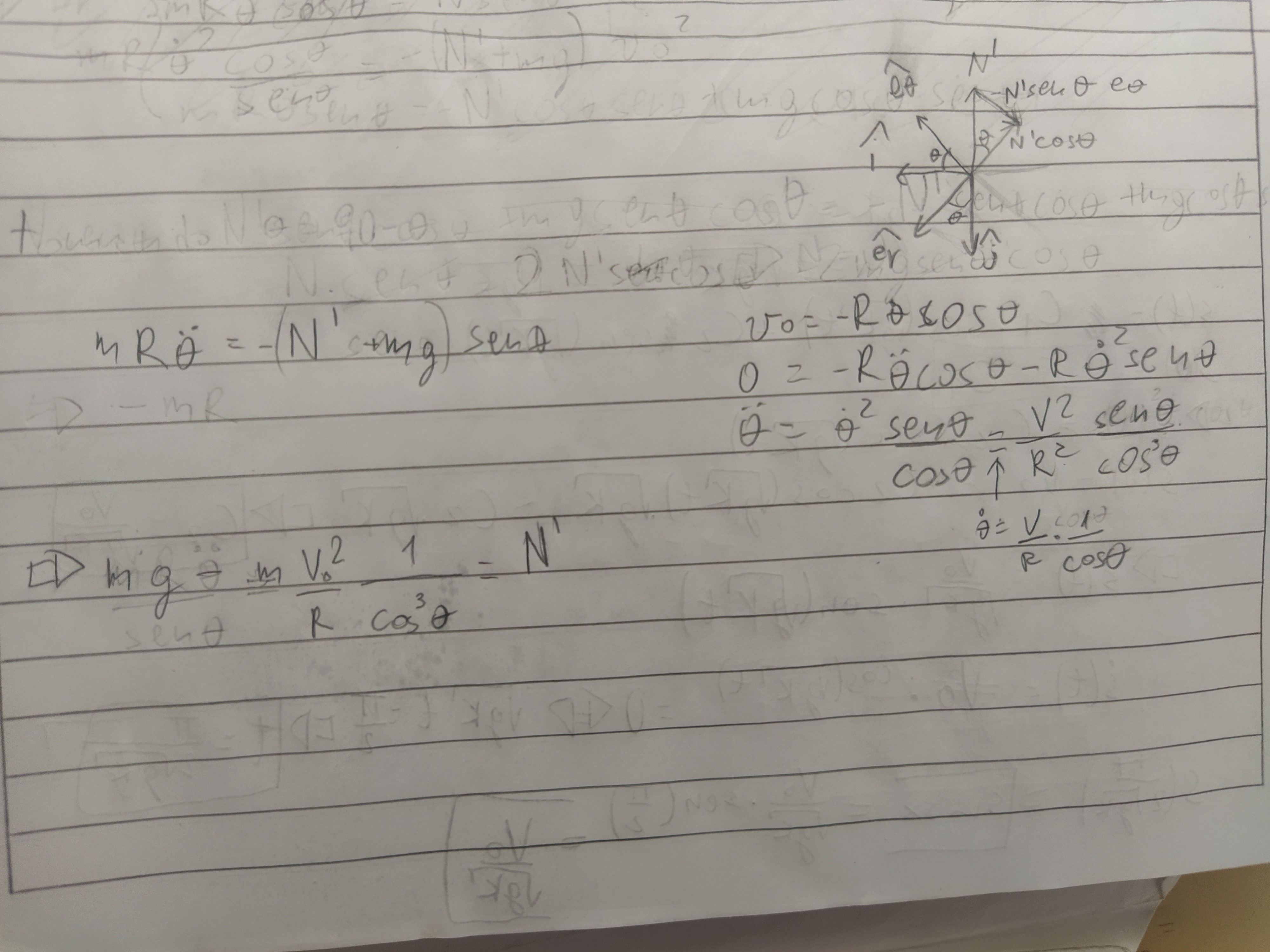Buenas, necesito una ayuda para poder representar las fuerzas en este ejercicio
Las fuerzas sobre el pasador A son: El peso, las reacciones normales de la ranura y la reacciòn normal de la guía B:
La idea del ejercicio es hallar la reacción 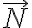 , la reacción que hace la guía B. Una forma de aislar esta fuerza sería tomar la proyección de la ecuación de movimiento en el versor
, la reacción que hace la guía B. Una forma de aislar esta fuerza sería tomar la proyección de la ecuación de movimiento en el versor 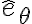 para sacarse de encima las otras reacciones que no nos piden:
para sacarse de encima las otras reacciones que no nos piden:
, pues las otras reacciones tienen componente únicamente en 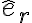 . Luego, intentá usar los datos que te da la letra: La velocidad está impuesta, es constante y en la dirección vertical:
. Luego, intentá usar los datos que te da la letra: La velocidad está impuesta, es constante y en la dirección vertical:
Esa velocidad y aceleración las podés describir por ejemplo en términos de la coordenada 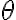 del dibujo. Estas condiciones impuestas en la ecuación de movimiento proyectada en la dirección tangencial a la ranura te van a permitir hallar la reacción normal de la guía B.
del dibujo. Estas condiciones impuestas en la ecuación de movimiento proyectada en la dirección tangencial a la ranura te van a permitir hallar la reacción normal de la guía B.
Muchas gracias!!
Hola,
1) tal como decís, la guía B aprieta al pasador en dos puntos de contacto. En cada punto de contacto (llamémosle a los mismos  y
y 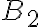 ) la guía ejerce sobre el pasador una reacción normal
) la guía ejerce sobre el pasador una reacción normal  y
y 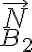 respectivamente. Sin embargo, lo que se puede averiguar es
respectivamente. Sin embargo, lo que se puede averiguar es 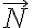 , la suma de estas normales:
, la suma de estas normales: 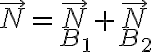 . El sentido de esta reacción resultante
. El sentido de esta reacción resultante 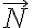 es dependiente de la forma en que se mueva el sistema: una vez que terminás el ejercicio podés darte cuenta de que apunta hacia arriba (en principio podrías suponer el sentido contrario a efectos de la 2da ley de Newton sobre el pasador y encontrarte al final con un Sg negativo, no hay problema).
es dependiente de la forma en que se mueva el sistema: una vez que terminás el ejercicio podés darte cuenta de que apunta hacia arriba (en principio podrías suponer el sentido contrario a efectos de la 2da ley de Newton sobre el pasador y encontrarte al final con un Sg negativo, no hay problema).
2) Al igual que la guía B que vimos antes, la ranura circular ejerce reacciones 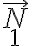 ,
, 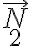 sobre el pasador en dos puntos de contacto. Aunque no es parte de lo que se pide en el problema, podrías eventualmente averiguar la suma de ellas:
sobre el pasador en dos puntos de contacto. Aunque no es parte de lo que se pide en el problema, podrías eventualmente averiguar la suma de ellas: 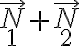 , la cual no es necesariamente cero, proyectando la 2da ley de Newton según la dirección radial de la ranura, donde en el término de fuerza vas a tener la proyección del peso del pasador, la proyección de
, la cual no es necesariamente cero, proyectando la 2da ley de Newton según la dirección radial de la ranura, donde en el término de fuerza vas a tener la proyección del peso del pasador, la proyección de 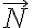 y
y 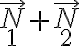 .
.
Saludos y espero que te haya aclarado la duda,
Ariel.
sii muchas gracias
Por alguna razón no llego al resultado de la solución. Es que la componente del peso y la normal en eθ me quedan multiplicadas por senθ. La solución me queda m.v^2/R.cos^3(θ).
Use el ángulo de la foto que mandaron por aca
Re: Use el ángulo de la foto que mandaron por aca
Hola,
Estas usando el ángulo complementario al que propone la letra. La proyección del peso y la Normal que tenés en la ec de Newton según 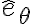 está bien. Tu error está en la proyección vertical de la velocidad que haces en la parte derecha de la hoja que mandaste. la velocidad es
está bien. Tu error está en la proyección vertical de la velocidad que haces en la parte derecha de la hoja que mandaste. la velocidad es 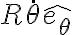 . Cuando la proyectas en la vertical te aparece coseno.
. Cuando la proyectas en la vertical te aparece coseno.
saludos
g
Re: Use el ángulo de la foto que mandaron por aca
Gracias, ahora si me quedo
Pd:Creo que hubo un error de tipeo en la ubicación de N_1 y N_2, no deberían estar según e_ro?
Gracias, saludos!
Ahí está usando el producto escalar con los vectores de la(s) base(s) para efectuar las proyecciones en los ejes correspondientes. Por ejemplo,
 corresponde a la componente según
corresponde a la componente según 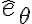 del vector
del vector 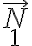 (¿sabrías demostrar esta afirmación?). Precisamente, como
(¿sabrías demostrar esta afirmación?). Precisamente, como 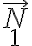 y
y 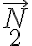 apuntan en la dirección de
apuntan en la dirección de 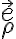 , el producto escalar con
, el producto escalar con 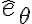 da cero autmáticamente.
da cero autmáticamente.En este sistema hay varias incógnitas:
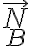 (que es lo que queremos hallar),
(que es lo que queremos hallar), 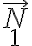 y
y 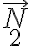 . Estás dos últimas no se pueden despejar por separado a partir de los datos, pero sí sería posible encontrar la suma
. Estás dos últimas no se pueden despejar por separado a partir de los datos, pero sí sería posible encontrar la suma 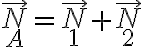 . Si lo pensamos como un sistema de dos incógnitas (
. Si lo pensamos como un sistema de dos incógnitas (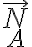 y
y 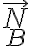 ), debe ser posible resolverlo proyectando en tu base predilecta (cartesiana o polar). El caso de proyectar en la base polar tiene la peculiaridad de que permite encontrar
), debe ser posible resolverlo proyectando en tu base predilecta (cartesiana o polar). El caso de proyectar en la base polar tiene la peculiaridad de que permite encontrar 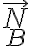 primero sin tener que hallar
primero sin tener que hallar 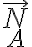 previamente.
previamente.Si obtuviste un sistema incompatible es posible que haya algún error de cuentas. ¿Quieres mandar cómo te quedó?
Saludos
NC
Ahora ya entendí.
Muchas gracias por tomarte el tiempo de contestar, salduos!