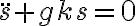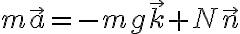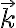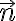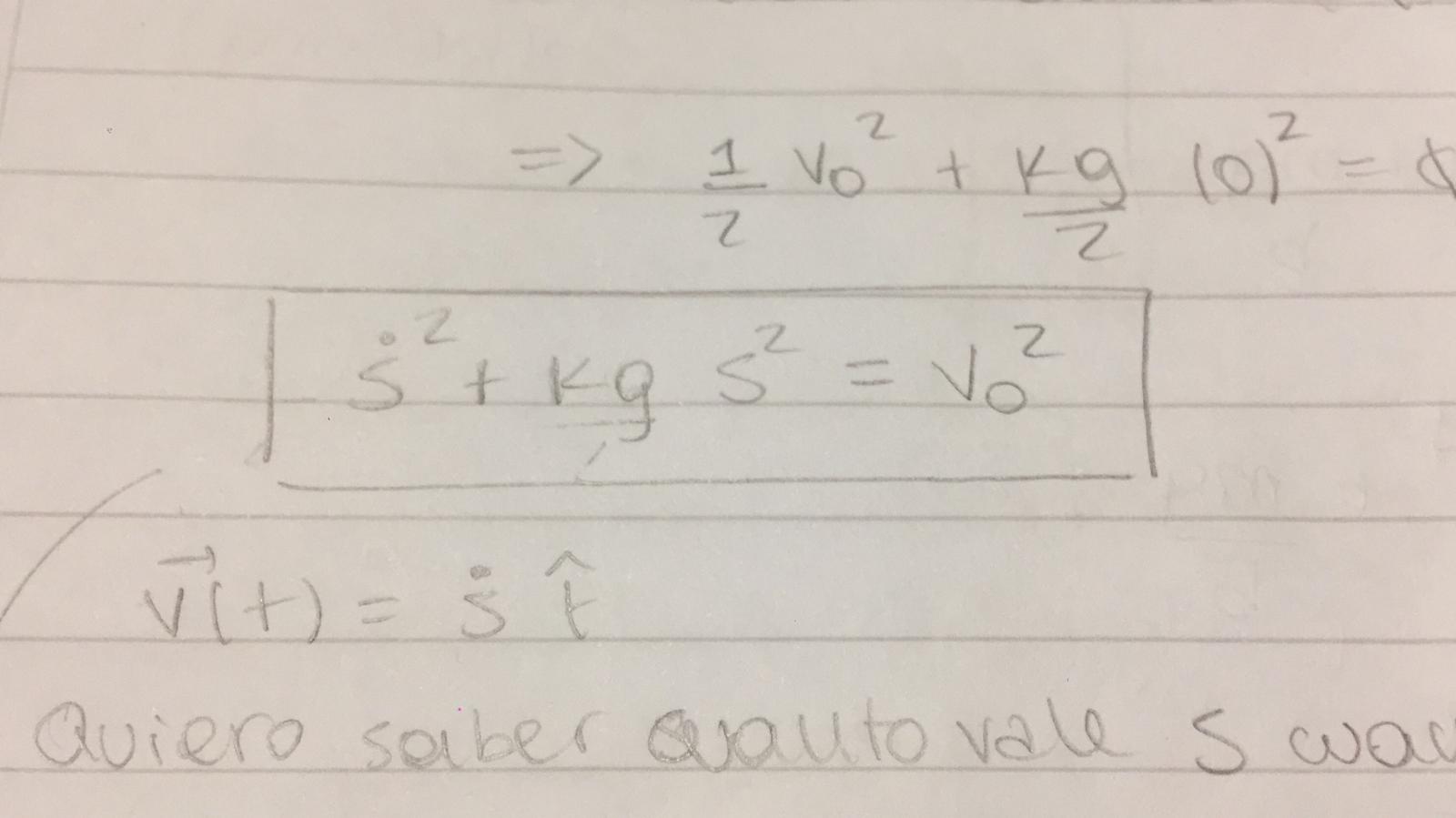
Hola Emilia. Por lo que veo, pareciera que llegaste correctamente a la ecuación de movimiento en la dirección tangencial, que es de la forma 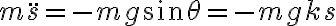 y luego la preintegraste.
y luego la preintegraste.
De ser así, te cuento que no es necesario en este caso, pues la ecuación que obtenés es fácilmente resoluble. De hecho tiene solución tipo sinusoidal (tal como se vio en Física 1).
Saludos!
Hola estaba haciendo el ejercicio y tuve la misma duda. No entiendo como hacer para, a partir de la ecuacuon de movimiento ( la misma que la foto de la compañera), llegar al tiempo que demora en detenerse.
Gracias
Hay dos formas:
De la preintegral de movimiento (que es la ecuación que muestra la compañera) se despeja 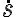 , que quedaría:
, que quedaría: ![\dot{s}= \sqrt[]{v_0^2-gks^2} \dot{s}= \sqrt[]{v_0^2-gks^2}](https://eva.fing.edu.uy/filter/tex/pix.php/e565a8d324177bdf1d74b727f32c2603.gif) . (Observar que la velocidad es positiva, porque s crece, ya que al aplicar la raíz hay dos signos posibles). Luego
. (Observar que la velocidad es positiva, porque s crece, ya que al aplicar la raíz hay dos signos posibles). Luego 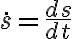 por lo que la ecuación se puede escribir como:
por lo que la ecuación se puede escribir como:
Se integra a la izquierda en s desde 0 (objeto en el origen) a la distancia hallada antes (máxima distancia recorrida hacia arriba, que es la distancia hasta que el objeto se detiene), y a la derecha en el tiempo, desde el instante inicial (0) al tiempo que demora en recorrer esa distancia, que es el tiempo que demora en detenerse, o sea, lo que se quiere hallar.
Por esta forma hay que conocer antes la distancia que recorre el objeto antes de detenerse, que es lo que pide primero el ejercicio, que es el valor de s para el cual  (distancia máxima implica derivada nula).
(distancia máxima implica derivada nula).
La otra forma, y que dice Inti, es directamente de la ecuación de movimiento, que es una ecuación diferencial lineal de segundo orden a coeficientes constantes homogénea, hallar la ley horaria s(t). En este caso la solución a esa ecuación diferencial es una combinación lineal de senos y cosenos con frecuencia angular ![\sqrt[]{gk} \sqrt[]{gk}](https://eva.fing.edu.uy/filter/tex/pix.php/4c997b31769bf40a040c0428313c21cd.gif) (Observar que las dimensiones o unidades son correctas). Para hallar las constantes de la combinación lineal hay que imponer condiciones iniciales: s(0)=0 y
(Observar que las dimensiones o unidades son correctas). Para hallar las constantes de la combinación lineal hay que imponer condiciones iniciales: s(0)=0 y 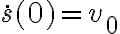 . Luego el instante en que la partícula se detiene es cuando
. Luego el instante en que la partícula se detiene es cuando  . Por este camino la distancia recorrida se halla después evaluando en la ley horaria para ese instante.
. Por este camino la distancia recorrida se halla después evaluando en la ley horaria para ese instante.
Estimado:
La ecuación da soluciones en senos y cosenos trigonométricos y no hiperbólicos porque la ecuación de movimiento a la que se llega es:
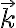 (el peso es descendente y el vector
(el peso es descendente y el vector 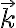 ascendente).
ascendente). 
![\frac{ds}{ \sqrt[]{v_0^2-gks^2 } } =dt \frac{ds}{ \sqrt[]{v_0^2-gks^2 } } =dt](https://eva.fing.edu.uy/filter/tex/pix.php/d7054425abe25e2643c411413a0cb064.gif)