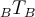Tengo una duda respecto al ejercicio 3, nos piden hallar los vaps y s.e ppios. de la matriz A y de la transformacion T, la letra indica que b(T)b = A por lo tanto, si yo encuentro los vaps de T, al ser b(T)b semejante a A, podria asumir que comparten los mismos vaps? y por ende s.e ppios.?
Aun no me queda muy clara la diferencia entre hallar los vaps de una transformacion y los vaps de una matriz.
Hola Diego.
De la proposición 37 (o corolario 38) y la definición 41 se desprende que los valores propios de una transformación y de cualquier matriz asociada a ella serán los mismos. Pero no así los vectores propios.
También por la proposición 37, y lo que se observa después de la definición 41, los vectores propios coinciden solo si se trata de la matriz asociada a la transformación lineal en la base canónica. Pues un vector propio de la matriz 
es el vector coordenada del vector propio de T en la base B.
Espero que haya ayudado.
Cualquier duda volvé a preguntar.
Saludos!
En conclusión, en el ejercicio 3 que nos piden hallar los vaps de A y de la t.l T, hallando los vaps de la matriz A puedo asumir que también son vaps de T? ya que A = b(T)b?
Exacto.
Lo que son distintos son los veps.
¿Ves por qué? Leé en el libro rojo las proposiciones, definiciones y observaciones que comenté antes.
Saludos