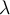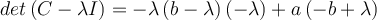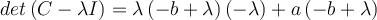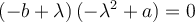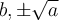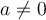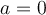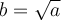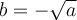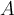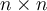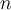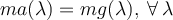Ejercicio 9

Ejercicio 9

de Romina Lopez Contrera -
Número de respuestas: 7

Hola, tengo dudas de cómo analizar los determinantes en función de a, b y lambda.

Sé que debo hallar los valores de lambda que hacen que el determinante sea igual a cero, pero me cuesta plantear los distintos casos usando a y b.

Si alguien tiene una idea de cómo encarar estos ejercicios lo agradezco, saludos!

En respuesta a Romina Lopez Contrera

Re: Ejercicio 9

de Matías Valdés -

Buenas.

¿Podrías pasar cómo te quedó el polinomio característico en funcón de los parámetros a y/o b?

Así te explicamos sobre un ejemplo concreto.

En general la idea es hallar las raíces \lambda en función de los parámetros a y/o b. Y una vez que se tiene esto, discutir para qué valores de los parámetros la matriz es diagonalizable.

Saludos.

Matías.
En respuesta a Matías Valdés

Re: Ejercicio 9

de Romina Lopez Contrera -

Hola, gracias por la respuesta, te muestro por ejemplo cómo me quedó el determinante de la parte c) 


Adjunto IMG_20200317_140856.jpg
En respuesta a Romina Lopez Contrera

Re: Ejercicio 9

de Annabella Zapattini -

Hola Romina.

Vos tenés det\left(C-\lambda I\right)=-\lambda\left(b-\lambda\right)\left(-\lambda\right)+a\left(-b+\lambda\right) que se puede escribir como: det\left(C-\lambda I\right)=\lambda\left(-b+\lambda\right)\left(-\lambda\right)+a\left(-b+\lambda\right) y podés factorizar, llegando a \left(-b+\lambda\right)\left(-\lambda^2+a\right)=0.

Se deduce que las raíces son b, \pm\sqrt{a}

De ahí tenés que discutir las distintas posibilidades. Una es, como alguien ya dijo, que los tres vaps sean distintos, entonces para este caso tendrías que exigir que a\neq 0 y estudiar aparte el caso a=0 (acá tendrías que ver cómo son las multiplicidades algebraicas y geométricas para ver si ese caso es posible o no).

Después también tendrías que ver qué sucede si b=\sqrt{a} o b=-\sqrt{a}, para ver si se les tiene que exigir algo más a a o b para que sea diagonalizable.

Espero que ayude el comentario.

Saludos
En respuesta a Romina Lopez Contrera

Re: Ejercicio 9

de Santiago Daniel Viera Silvera -

Buenas, después de que encuentres los valores propios, tenes que analizar los casos en que sean distintos o iguales entre si (si todos los valores propios son distintos entonces la matriz es diagonalizable).

Por ejemplo si λ1 = 1, λ2= a, λ3= -a, tenes que discutir los siguientes casos:

a ≠ -a ≠ 1 (los tres distintos)

a = -a ≠ 1 (o sea a = 0)

a ≠ -a = 1 (o sea a = -1)

a = 1 ≠ -a (o sea a = 1)

a = -a = 1 (caso imposible) ( creo que no me olvide de ninguno).

Despues de analizar los casos, para los valores propios con multiplicidad mayor a 1, tenes que hallar el subespacio propio de esos valores y ver que dimension tiene.

Acordate que 1≤MG(λ)≤MA(λ), y  si MA(λ) = MG(λ) entonces la matriz es diagonalizable.

No se que parte del ejercicio 9 hiciste asi que te di un pantallazo general. 

Matias se podrias fijate si no puse algo mal, por las dudas.


En respuesta a Santiago Daniel Viera Silvera

Re: Ejercicio 9

de Matías Valdés -

La única aclaración que agregaría a tu razonamiento es que, para que A sea diagonalizable, la igualdad entre multiplicidad algebraica y geométrica debe darse para todos los valores propios de A (no basta con que se cumpla para uno o algunos de los valores propios de A). Esto es:

A matriz n \times n es diagonalizable si y sólo si A tiene n valores propios (posiblemente repetidos) y se cumple: ma(\lambda) = mg(\lambda), \: \forall \: \lambda

Saludos.

Matías.