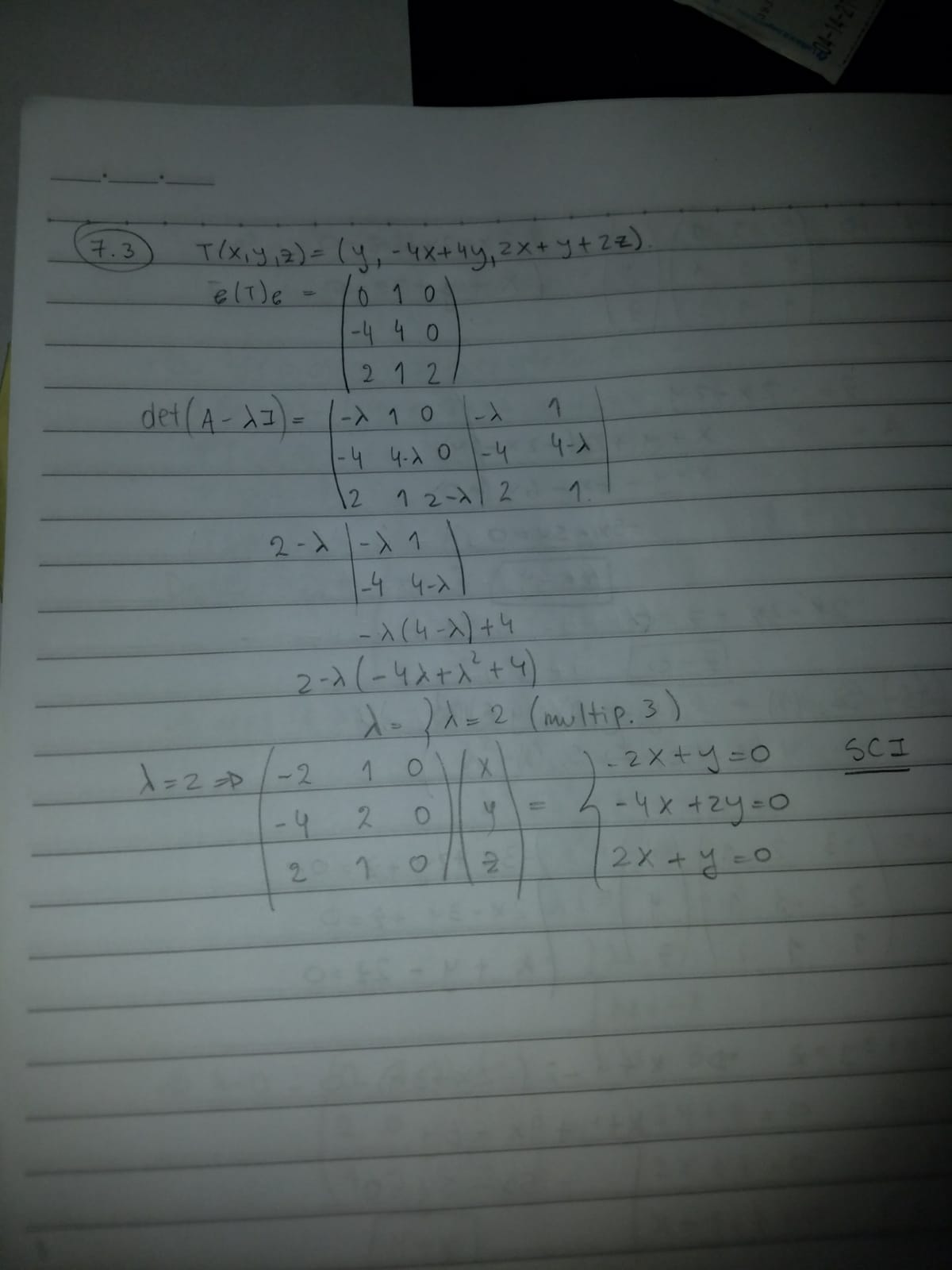Que significa que la unica solucion es la trivial? Significa que el Subespacio solamente esta formado por el vector nulo?
Así es, que la única solución sea la trivial significa que la única solución es el vector nulo.
Pero el sistema sistema que muestras en la foto tiene solución no trivial de hecho
Sol(S)=S2={(0,0,z): z real}
Saludos,
Florencia.
Segun la primer ecuacion 2x = y, si sustituis en la tercera te da 4x = 0 por lo tranto x=0 sino seria un sistema incompatible no?
x=0 e y=0 (yo había leído mal, ya está corregido), pero sobre z no tienes condiciones, esto quiere decir que z puede ser cualquiera.
Buenas.
Tu procedimiento y tus cuentas parecen estar bien.
De todas formas el sistema tiene infinitas soluciones. Esto es porque, si bien de las ecuaciones se deduce que debe ser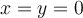 
, estas no te imponen restricciones sobre la coordenada 
.
Por lo tanto el subespacio propio (de la matriz asociada) es: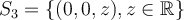 
. En este caso coincide con el subespacio propio de T, por estar usando la base canónica.
Como comentario general: los subespacios propios siempre tienen dimensión al menos 1. En particular esto quiere decir que: si llegaste a que el subespacio propio es el subespacio trivial, entonces hiciste algo mal.
Saludos.
Matías.