La única aclaración que agregaría a tu razonamiento es que, para que A sea diagonalizable, la igualdad entre multiplicidad algebraica y geométrica debe darse para todos los valores propios de 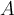 (no basta con que se cumpla para uno o algunos de los valores propios de
(no basta con que se cumpla para uno o algunos de los valores propios de  ). Esto es:
). Esto es:
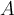 matriz
matriz 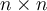 es diagonalizable si y sólo si
es diagonalizable si y sólo si 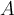 tiene
tiene 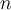 valores propios (posiblemente repetidos) y se cumple:
valores propios (posiblemente repetidos) y se cumple: 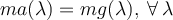
Matías.