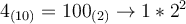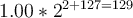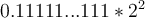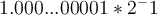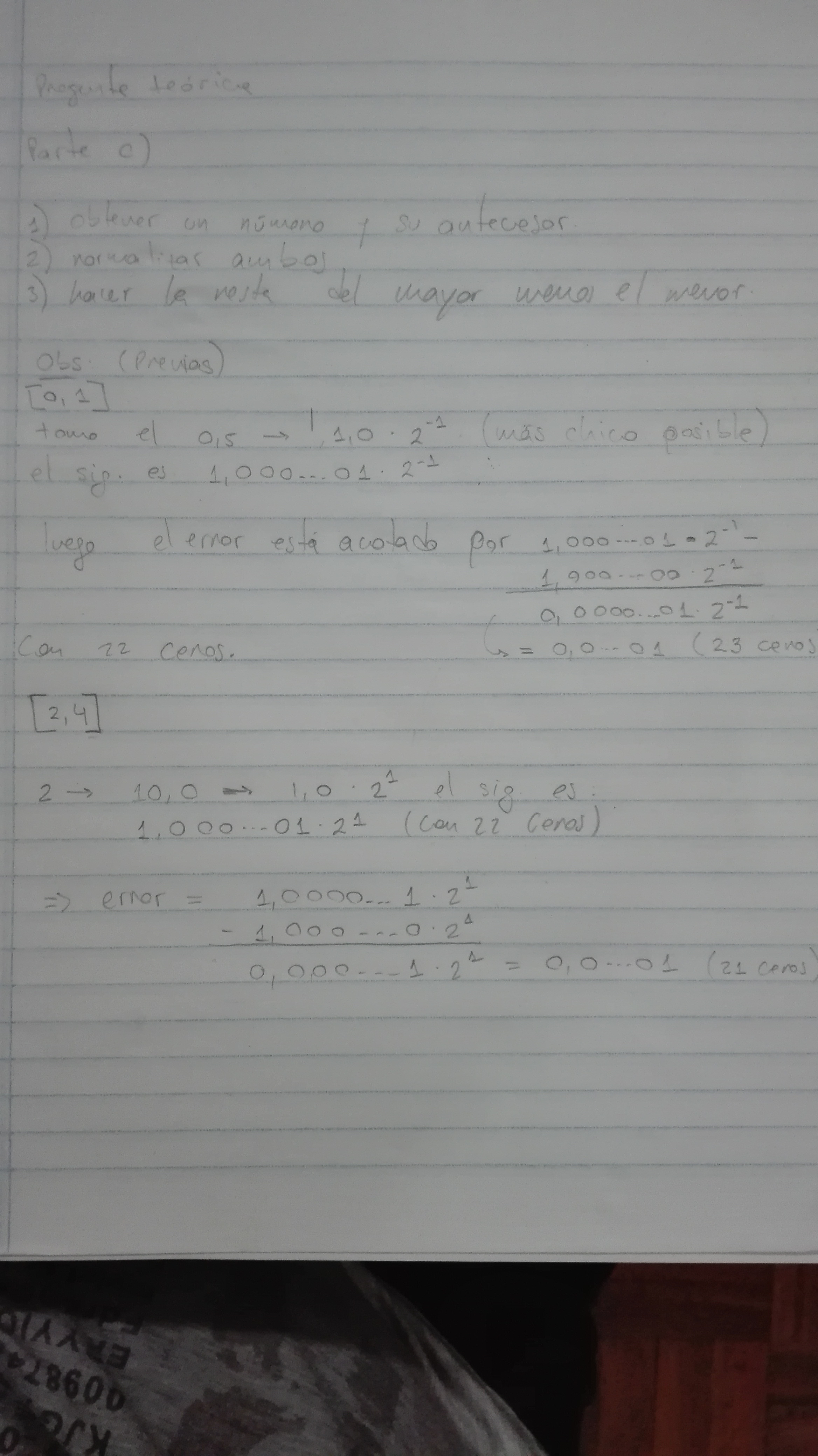En esta pregunta entiendo que la cota superior para el error de representación, por ejemplo del intervalo [0,1] o [2,4] es buscar cual es la diferencia entre 4 y el antecesor más próximo representable.
Es decir
en punto flotante 
luego el número anterior en la representación es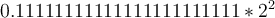 
si resto la representación del cuatro menos su antecesor obtengo la diferencia 
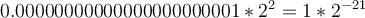, y así con los demás intervalos
Quisiera saber si está bien este razonamiento,
Gracias!
Estimado:
La idea está bien. Lo único que ese caso en particular no te sirve porque el número 4 y su antecesor en PF tienen diferente exponente (4 decimal se escribe 1.000...0 * 2^2 y su antecesor es 1.1111111...11111 * 2^1), en ese sentido, están mal expresados los intervalos en la letra, sería [2,4).
Si tomás dos números cualquiera del mismo intervalo de exponente todo lo demás que planteaste es correcto!
Saludos,
Federico
Razonando de la misma manera para el intervalo [0,1], puedo tomar el 0.5 = 0.1 x 2^0
y restarle su antecesor 0.0111 x 2^0 para llegar a que la cota superior para el error es 0.0001 = 1x2^-4 ?
Estimado:
Algo que ahora veo no corregí en su momento, es que los números los tenés que expresar en formato punto flotante normalizado (ver que usé la notación 
en lugar de 
.
De ese modo, el 0.5 se expresa como 1.0 * 2^-1, y es el punto flotante más chico que se obtiene con el exponente -1, el siguiente serìa: 
, con 22 ceros (porque la mantisa en simple precisión tiene 23 bits. Por esta razón, el error está acotado por la diferencia: 
.
En tu caso, aparte de lo que indiqué, es incorrecto el antecesor.
Saludos,
Federico
Hola, ¿cómo puedo asegurar que no hay un error mayor entre algún par dentro del intervalo?
¿por qué debo tomar el mayor del intervalo y su antecesor? no me queda muy clara esta parte.
[edit] o sea, tampoco puedo tomar 1 y su antecesor, porque sería cambiarle el exponente. En este caso debo tomar desnormalizados? [/edit]
Saludos
Seria esta la idea...
Hola!
¿cómo puedo asegurar que no hay un error mayor entre algún par dentro del intervalo?
Hay que ver primero que como la mantisa es de la forma 1.F, la mantisa toma valores entre 1.000...0000 = 1 y 1.11111....111 que es casi 2. Por lo tanto, una vez fijo el exponente E, al variar la mantisa los números siempre están en el intervalo [ 2^E, 2^E+1 )Y esos números distan lo mismo entre ellos, exactamente 2^E * 1.0000...000001, por lo tanto el error es constante en el intervalo.
¿por qué debo tomar el mayor del intervalo y su antecesor? no me queda muy clara esta parte.
No es necesario, con tomar dos cualesquiera del intervalo, ya está (ver punto anterior)Saludos,
Federico