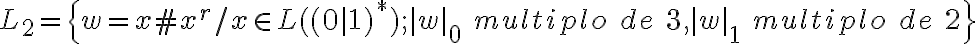Hola, mi duda es cuando se toman el Z en la solución para el contrareciproco del P.L.
Ustedes se dan un Z=1^N #1^N
Pero según letra debe haber cantidad par de 1s en X. ¿Debería decir para cualquier N par?
Gracias, dejo link al examen: https://www.fing.edu.uy/inco/cursos/teoleng/examenes/TL-Diciembre2015.pdf
Solucion: https://www.fing.edu.uy/inco/cursos/teoleng/examenes/ST-Diciembre2015.pdf
Fijate que en la solución (en la letra sí está como decís) dice: 
, es decir, la cantidad de 1's en toda la tira es par, y el z que proponen tiene 2N 1's.
Probablemente hayan avisado del cambio de letra en el parcial, pero no lo modificaron en el pdf.
Saludos.
hola:
una aclaración: uno no puede elegir el N, porque, precisamente, se debe probar el "para todo"; la frase "para N par" estaría mal, porque no probarías el contrarrecíproco para todos los N impares.
lo que uno sí puede elegir es la tira z. entonces, si la letra fuese |x|1 mult 2 (en lugar de w), dado N, se podría elegir, por ejemplo, 1^2N # 1^2N o 1^M #1^M, siendo M un número par mayor o igual a N.
saludos,
d.-
Gracias a ambos