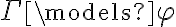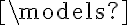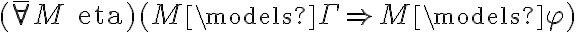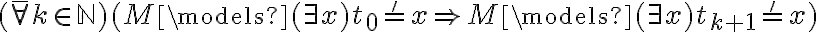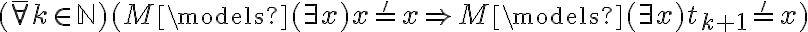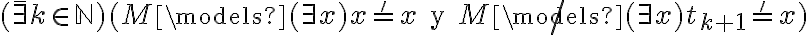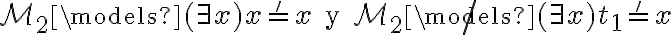Parciales

Creo que ahora entendí mejor por qué venía tu duda de hacer el cambio de variable.

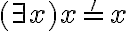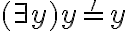Si quisieras cambiar la variable, podrías, pero primero tenés que remplazar t₀ por lo que realmente significa, entonces pasarías de $(\exists x) x =' x$ a $(\exists y) y =' y$ (o con la variable que eligieras). Lo mismo con t_k+1, si la variable del cuantificador cambiara, la de adentro del término también.

"¿En la parte derecha puede haber cualquier cosa y no cambia el ejercicio?" no, cambia sí.

$\Gamma \models \varphi$ sii [def $\models$] $(\bar{\forall} M \text{ eta} ) ( M \models \Gamma \Rightarrow M \models \varphi )$.

El único caso en que no importa la parte derecha, es cuando la parte izquierda es falsa en todas las estructuras. Pero no es el caso de este ejercicio.

Si la frase fuera verdadera, habría que probar:

para toda estructura M, $(\bar{\forall} k \in \mathbb{N}) ( M \models (\exists x)t_0 =' x \Rightarrow M \models (\exists x) t_{k+1} =' x)$

Sustituyendo t₀ por lo que realmente significa:

para toda estructura M, $(\bar{\forall} k \in \mathbb{N}) ( M \models (\exists x) x =' x \Rightarrow M \models (\exists x) t_{k+1} =' x )$

Como el antecedente es verdadero en todas las estructuras (hay que probarlo, pero es fácil ver que es verdadero), la implicancia va a ser verdadera sii el consecuente siempre es verdadero. Pero no siempre lo es. La frase es falsa.

Hay que buscar un contraejemplo, esto es, mostrar que se cumple que

existe estructura M, $(\bar{\exists} k \in \mathbb{N}) ( M \models (\exists x) x =' x \text{ y } M \not\models (\exists x) t_{k+1} =' x )$.

Hay que elegir un M y un k que no modelen el consecuente.

Recomiendo elegir k = 0 y M = M2, el de la parte bI. Probar:

$\mathcal{M}_2 \models (\exists x) x =' x \text{ y } \mathcal{M}_2 \not\models (\exists x) t_1 =' x$

(observar que parte de la justificación ya está hecha en el ejercicio bI, no hace falta repetirla).

Saludos