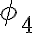Acordate que para calcular un flujo la superficie primero debe estar orientada, vos al usar la parametrización que te da la letra tenés que calcular 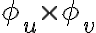 y ver si ese vector también tiene tercera coordenada negativa, si es así la parametrización preserva orientación y estás efectivamente calculando el flujo sobre
y ver si ese vector también tiene tercera coordenada negativa, si es así la parametrización preserva orientación y estás efectivamente calculando el flujo sobre  , si no es así, la parametrización está revirtiendo la orientación, y en verdad estás calculando el flujo sobre
, si no es así, la parametrización está revirtiendo la orientación, y en verdad estás calculando el flujo sobre 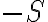 , y por las propiedades de los flujos esos 2 son opuestos, o sea que si hacés las cuentas con una parametrización que revierta orientación al final tenés que cambiarle el signo al resultado.
, y por las propiedades de los flujos esos 2 son opuestos, o sea que si hacés las cuentas con una parametrización que revierta orientación al final tenés que cambiarle el signo al resultado.
Por otro lado, al aplicar Stokes no te olvides que a 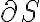 tenés que darle la orientación borde, que es la siguiente: mirás la normal
tenés que darle la orientación borde, que es la siguiente: mirás la normal  en un punto del borde y en ese mismo punto elegís un vector
en un punto del borde y en ese mismo punto elegís un vector  tangente a la curva (hay 2 posibles, con sentidos opuestos), si al hacer la regla de la mano derecha yendo de
tangente a la curva (hay 2 posibles, con sentidos opuestos), si al hacer la regla de la mano derecha yendo de  a
a  por el ángulo más corto quedás apuntando hacia la superficie, entonces el vector
por el ángulo más corto quedás apuntando hacia la superficie, entonces el vector  que elegiste efectivamente te está indicando la orientación borde de
que elegiste efectivamente te está indicando la orientación borde de 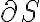 , si no es así, tenés que orientar
, si no es así, tenés que orientar 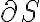 según
según 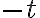 .
.
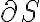 tiene siempre tercera componente nula, entonces al calcular la circulación de
tiene siempre tercera componente nula, entonces al calcular la circulación de  sobre
sobre 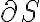 (ya que la idea es aplicar Stokes) esa componente nula me mata la tercera componente del campo al hacer el producto escalar, por lo tanto no preciso saberla.
(ya que la idea es aplicar Stokes) esa componente nula me mata la tercera componente del campo al hacer el producto escalar, por lo tanto no preciso saberla.
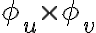



![[\frac{\pi}{2}, 0] [\frac{\pi}{2}, 0]](https://eva.fing.edu.uy/filter/tex/pix.php/4ef263506542aa4cf6a031fa022c3670.gif)

![[-\frac{\pi}{2},0] [-\frac{\pi}{2},0]](https://eva.fing.edu.uy/filter/tex/pix.php/394f82a7351b6a5251bc2cd907bac265.gif)