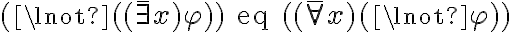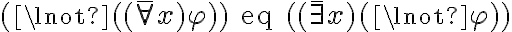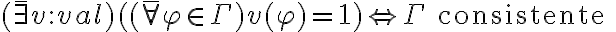Condición suficiente de consistencia

Condición suficiente de consistencia

de Nicolas Gerardo Perez Alano -
Número de respuestas: 1
Una consulta, el contra reciproco de la condición suficiente de consistencia, dice: que si existe una valuación v que cumple que v(a)=0 para todo a perteneciente al conjunto entonces es inconsistente??? o dice que si no se cumple la condición suficiente de consistencia ya es inconsistente??
En respuesta a Nicolas Gerardo Perez Alano

Re: Condición suficiente de consistencia

de Romina Romero - InCo -

Hola.

No, no dice eso.

Vos tenés que negar un existe. La negación de "existe alguien (X) que cumple algo" es "no existe nadie que lo cumpla", o sea "para todo X, X no cumple algo".

(\lnot ((\bar{\exists} x) \varphi)) \text{ eq } ((\bar{\forall} x)(\lnot \varphi))

Que exista una valuación que no lo cumpla no alcanza, porque capaz que elegiste la valuación equivocada.

Ejemplo

Consideremos la siguiente afirmación: "tengo un amigo que estudia economía".

Lo formalizo como "existe X amigo mío, X estudia economía" (1).

Te presento a Pepito, mi amigo, que estudia ingeniería (2). ¿Podés asumir que no tengo amigos en economía?

Transformo (2) para formalizar: "mi amigo Pepito no estudia economía" (3).

Si (1) es falso, no alcanza con decir "existe X amigo mío, X no estudia economía" * (formalización de (3)), porque puedo tener más de un amigo, uno en ingeniería y otro en economía.

Tengo que probar que "para todo x amigo mío, x no estudia economía".


De igual forma, la negación de "para toda fórmula phi, v(phi) = 1", no es que todas valgan 0, sino que alguna valga 0.

(\lnot ((\bar{\forall} x) \varphi)) \text{ eq } ((\bar{\exists} x)(\lnot \varphi))


Por otro lado, las condiciones suficientes no son siempre "necesarias", por lo que el contrarrecíproco no funciona como lo estás aplicando. Una condición suficiente dice:

si condición suficiente => propiedad

El contrarrecíproco queda:

NO propiedad => NO condición suficiente.

Ejemplo (propiedad: ser múltiplo de 2)

si n es múltiplo de 4 => n es múltiplo de 2

n no es múltiplo de 2 => n no es múltiplo de 4

Es suficiente saber que es múltiplo de 4, para saber que es múltiplo de 2, pero capaz que no es imprescindible (6 no es múltiplo de 4).


Vos lo que querés es un contrarrecíproco de la forma:

NO condición => NO propiedad

y esto es para una condición necesaria: si propiedad => condición necesaria.

Ejemplo (propiedad: ser múltiplo de 2)

si n es múltiplo de 2 => n es entero

n no es entero => n no es múltiplo de 2

Es necesario ser entero para ser múltiplo de 2, pero capaz que no alcanza (1 es entero).


En este caso, la condición además de ser suficiente, es necesaria. O sea, es un si y solo si:

(\bar{\exists} v : val)((\bar{\forall} \varphi \in \Gamma) v(\varphi) = 1) \Leftrightarrow \Gamma \text{ consistente }

Pero lo que te sirve para decir que es inconsistente es el contrarrecíproco de la necesidad, no de la suficiencia.


Si no entendés algo, avisá.


Saludos


* Obs. que el lenguaje natural se ordena un poco distinto que el formal. Formalmente sería 'no x_estudia_economía', donde x_estudia_economía es una proposición atómica.