Foro de dudas del práctico 3

La expresión de F a la que llegás es correcta. Hay que aclarar que 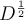$D^{\frac{1}{2}}$ consiste en tomar la raíz cuadrada de los elementos de la matriz diagonal D. La idea del ejercicio es poder generalizar la noción de "raíz cuadrada" para una matriz no diagonal (diagonalizable).

No estoy seguro si el razonamiento mediante el cual llegas a F es correcto. Si la expresión 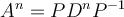$A^{n}=PD^{n}P^{-1}$ la probaste mediante inducción completa, entonces sólo es válida para n natural. Es decir que no podrías usar $n= \frac{1}{2}$.

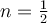Una alternativa para obtener F es escribir: 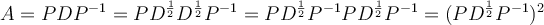$A = PDP^{-1} = P D^{\frac{1}{2}} D^{\frac{1}{2}} P^{-1} = P D^{\frac{1}{2}} P^{-1}P D^{\frac{1}{2}} P^{-1}= ( P D^{\frac{1}{2}} P^{-1} )^{2}$. Por lo tanto 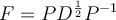$F=PD^{\frac{1}{2}}P^{-1}$ como antes.

Saludos.

Matías.