Buenas, no me doy cuenta de que están pidiendo en este apartado.
(Desde lo que logré interpretar) no logré ver una perspectiva clara para acercarme al ejercicio, alguna idea?
Saludos, Francisco.
Buenas, no me doy cuenta de que están pidiendo en este apartado.
(Desde lo que logré interpretar) no logré ver una perspectiva clara para acercarme al ejercicio, alguna idea?
Saludos, Francisco.
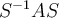 y
y  son los mismos y la parte anterior.
son los mismos y la parte anterior.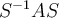 y
y  son los mismos, cualquier aproximación que hagas para un valor propio de
son los mismos, cualquier aproximación que hagas para un valor propio de 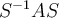 sirve para los valores propios de
sirve para los valores propios de  (porque son los mismos).
(porque son los mismos).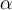 para que el radio del primer circulo (
para que el radio del primer circulo (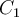 ) de
) de 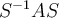 sea tan pequeño como sea posible sin que se interseque con los otros dos circulos, es decir para ese
sea tan pequeño como sea posible sin que se interseque con los otros dos circulos, es decir para ese 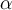 tenés que
tenés que 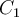 no se corta con los otros dos circulos y entonces podés usar el teorema de Gerschgorin para aproximar dentro de
no se corta con los otros dos circulos y entonces podés usar el teorema de Gerschgorin para aproximar dentro de 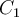 el primer valor propio de
el primer valor propio de 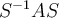 , y por lo tanto el primer valor propio de
, y por lo tanto el primer valor propio de  . Además elegiste
. Además elegiste 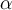 para que el circulo sea tan pequeño como sea posible.
para que el circulo sea tan pequeño como sea posible.