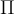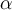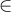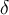Cal3: ejercicio 2 M.O primer parcial 2013

No me doy cuenta como resolver este ejercicio que corresponde a el primer parcial de 2013

Dado el campo X : R² → R², se sabe que es irrotacional y que X (t, 0) = (2t + 1, 1) para todo t ∈ R, y la curva {(x, y) ∈ R2: x2+ y2= 1, y ≥ 0} recorrida en sentido antihorario. Entonces∫_C X =???

la parametrización es la circunferencia entre 0 y $\Pi$ $\alpha$ (t) = (cos(t),sen(t)) con t $\in$ [0, $\Pi$ ]
, el rotor da 0 por lo que al ser un rotor de un campo plano si X=(P,Q) ==>- $\delta$ P/ $\delta$ y + $\delta$ Q/ $\delta$ x =0 y por los datos $\delta$ Q/ $\delta$ x =0 pero no se como seguir avanzando

Re: ejercicio 2 M.O primer parcial 2013

de Gabriel Núñez - miércoles, 9 de diciembre de 2015, 19:36

Hola Andrea,

Dado que el campo es irrotacional y esta definido en R^2 se obtiene que la integral no depende del camino. Por tanto hallar la circulación a través de la media cfa es lo mismo que ir vía el segmento en el eje x.

Ahora, la circulación en dicho segmento podes calcularlo, porque tenes exactamente cómo es el campo en TODO el eje x.

Haciendo esto deberías llegar al resultado. Cualquier cosa que no se entienda pregunta, saludos

Gabriel