Alguien puede explicarme como se hace la parte 1 donde piden la velocidad angular de la esfera? Me fijé en la solución, pero sigo sin entender, gracias!
Voy transcribiendo la solución y esclareciendo un poquito las partes que me parecen más confusas:
"La velocidad angular de la esfera la podemos escribir
como,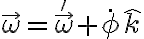
donde 
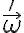es la velocidad angular de la esfera relativa al casquete."
Acá está usando el teorema de adición de velocidades angulares. Lo que quiere decir es que la velocidad angular de la esfera es la del casquete más la velocidad angular de la esfera "vista desde el casquete".
"Como la velocidad relativa de los puntos de contacto es nula,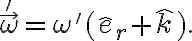
"
La explicación de esto está en el ejercicio 7 del práctico 5. Dice que la velocidad angular de un rígido que tiene dos puntos fijos, es colineal con la recta en la que están contenidos. En este caso, los puntos de contacto están fijos en un sistema relativo al casquete. Por lo tanto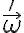 es colineal con el vector que une esos dos puntos, o sea la dirección 
.
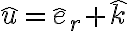Después el resto es cuentas.
Saludos :)
"La velocidad angular de la esfera la podemos escribir
como,
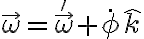donde 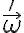es la velocidad angular de la esfera relativa al casquete."Acá está usando el teorema de adición de velocidades angulares. Lo que quiere decir es que la velocidad angular de la esfera es la del casquete más la velocidad angular de la esfera "vista desde el casquete".
"Como la velocidad relativa de los puntos de contacto es nula,
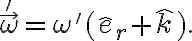"La explicación de esto está en el ejercicio 7 del práctico 5. Dice que la velocidad angular de un rígido que tiene dos puntos fijos, es colineal con la recta en la que están contenidos. En este caso, los puntos de contacto están fijos en un sistema relativo al casquete. Por lo tanto
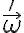es colineal con el vector que une esos dos puntos, o sea la dirección 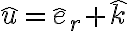.Después el resto es cuentas.
Saludos :)
En ese mismo ejercicio, en la parte 3 que calcula el momento angular. Cuando hace el momento angular de el casquete entiendo, pero el de la esfera no. No entiendo de donde sale el segundo termino
El de la esfera lo calcula con la fórmula de L para sist. de partículas , queda para la esfera:
L (en O) = L (en G) + .....
El L en G lo calculás con la fórmula para L en rígidos.
Saludos.
L (en O) = L (en G) + .....
El L en G lo calculás con la fórmula para L en rígidos.
Saludos.
Me surge una duda, con respecto a los ... ahi seria P^(O-G)
siendo P= m*Vcm, la velocidad de G, no sería r(fi punto+ tita punto) segun e tita? y ahi la solución no queda el termino de m*r^2* tita punto. Que es lo que está mal? porque no me doy cuenta.
Gracias!
siendo P= m*Vcm, la velocidad de G, no sería r(fi punto+ tita punto) segun e tita? y ahi la solución no queda el termino de m*r^2* tita punto. Que es lo que está mal? porque no me doy cuenta.
Gracias!
La velocidad de G que decís depende solamente de la velocidad con la que gira la esfera en relación al casquete, porque la estás viendo desde el centro del casquete que ya está girando con una velocidad (que en el sistema desde el cual estás viendo sería la misma, entonces no cuenta esa velocidad).
vG = R* (fi).
según efi siendo fi punto la velocidad angular de el G de la esfera respecto de O (es una velocidad relativa, no absoluta).
vG = R* (fi).
según efi siendo fi punto la velocidad angular de el G de la esfera respecto de O (es una velocidad relativa, no absoluta).
Si pero la velocidad del punto O es cero, no se te cancela el otro termino? En la solucion toma la velocidad de G y la formula es con la de O
Lo que pasa es que son velocidades diferentes porque salen de ecuaciones diferentes (una la L de sist. de partículas y otra de L de rígidos)
Para calcular L en G vas a la formula de rigidos y (luego de proyectar la w de la parte 1 segun k) solo sobrevive el termino de II*w donde w es la velocidad de la esfera que hallaste en la parte 1.
El resto de la expresión (los que antes puse como ...) son de la formula de L en sistemas de particulas, ahi ese producto vectorial de P con (O - G) es relativo entre la esfera y el casquete, por lo tanto v en G es la relativa, no la absoluta.
Por lo que yo entiendo en la parte 1 te piden la velocidad angular absoluta de la esfera, pero en la formula de L en sistema de particulas se usan las velocidades relativas entre los 2 puntos que quieras calcular el L.
Para calcular L en G vas a la formula de rigidos y (luego de proyectar la w de la parte 1 segun k) solo sobrevive el termino de II*w donde w es la velocidad de la esfera que hallaste en la parte 1.
El resto de la expresión (los que antes puse como ...) son de la formula de L en sistemas de particulas, ahi ese producto vectorial de P con (O - G) es relativo entre la esfera y el casquete, por lo tanto v en G es la relativa, no la absoluta.
Por lo que yo entiendo en la parte 1 te piden la velocidad angular absoluta de la esfera, pero en la formula de L en sistema de particulas se usan las velocidades relativas entre los 2 puntos que quieras calcular el L.
Mi pregunta es la siguiente, haciendo la cuenta que hace en la solucion, no calcula el momento angular de la esfera desde G?
Porque yo lo que hice fue calcular el tensor de inercia de la esfera desde el punto O y multicplicarlo por omega. Esa cuenta no me da lo mismo que la solucion. Que le estoy errando? Uso la omega que calcule en la parte 1. De esa cuenta solo me quedo con lo que queda segun k porque es lo que me piden.
Buenazo, gracias!