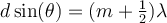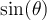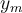Estimados foristas sigo con la problematica que me presenta el practico de referencia y en el RHK encuentro la separacion entre los maximos que es la misma que entre los minimos, sin embargo si tengo la ubicacion para hallar un ym emesimo maximo (41-3), pero como hallo el ym emesimo MINIMO? dado que hallando esta distancia puedo hacer y9 - y0 y obtener lambda. Tengo en la cabeza colocar m + 1/2 pero sin respaldo matematico, solo la conjetura que es el indice que se desprende en los minimos. Espero haber sido claro en lo que deseo, las disculpas del caso si no.
saludos sebastian./