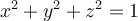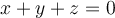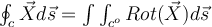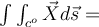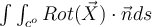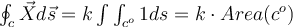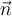Foro

Si yo tengo una curva dada por la intersección de dos superficies, digamos, por ejemplo:

$x^2+y^2+z^2=1$

$x+y+z=0$

Yo puedo calcular $\oint_c \vec{X} d\vec{s} = \int \int_{c^o} Rot(\vec{X}) d\vec{s}$

Además 

$\int \int_{c^o} \vec{X} d\vec{s} =$ $\int \int_{c^o} Rot(\vec{X}) \cdot \vec{n} ds$

En el caso de que 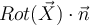$Rot(\vec{X}) \cdot \vec{n}$ es una constante 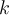$k$ tengo que:

  $\oint_c \vec{X} d\vec{s} = k \int \int_{c^o} 1 ds = k \cdot Area(c^o)$

Mi problema es que creo que hasta ahora siempre que me pasaba eso y usar esa propiedad me facilitaba las cuentas siempre las normales eran del estilo: 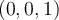$(0,0,1)$ o $(0,0,-1)$

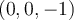
En el caso de esta curva, la normal es 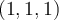$(1,1,1)$ y si no la normalizo (no sé si está bien usado el término, pero me refiero a dividir entre la norma 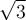$\sqrt{3}$) me da un resultado, si la normalizo me da otro.

Agradezco aclaración, saludos.