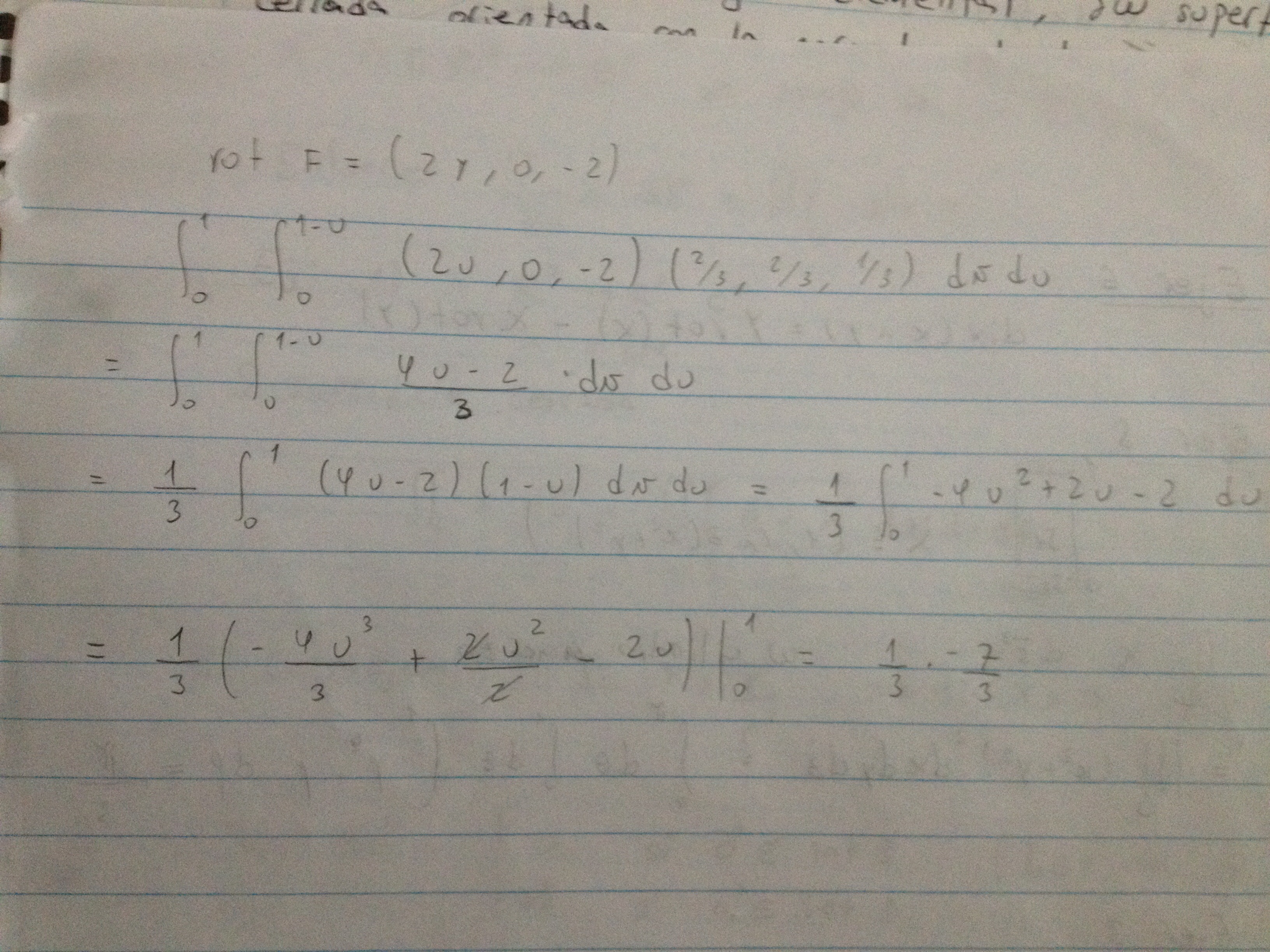Estoy teniendo el mismo problema cada vez que se me presenta la obligación de parametrizar una parte de un plano no trivial.
Por ejemplo:
Sea 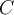 el contorno del triángulo con vértices en
el contorno del triángulo con vértices en 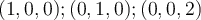
Mi interes es parametrizar el interior del triángulo como motivación a aplicar Stokes en un problema 
Por GAL, yo sé que dos rectas generan un plano.
son las rectas de "los costados" del triángulo, por ende, combinaciones lineales de esas rectas generarían todo el plano que contiene el triángulo.
Debería ser una parametrización válida de lo que busco, no? Porque nunca me dan bien los resultados finales y supongo que el error tiene que estar aca. Gracias.
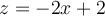
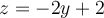
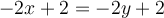
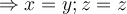
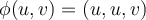
![u=[0,1], v=[0,2] u=[0,1], v=[0,2]](https://eva.fing.edu.uy/filter/tex/pix.php/1e0611afa2650fad2d4768b7cb9ccbe0.png)