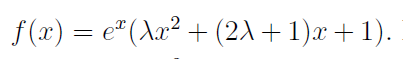Cal1: Posible error en solucion de julio examen 2012

Segun las soluciones dadas por los profesores, la correcta es la D.

Para mi esta mal y voy a explicar porque:

Sea z=A+Bi

(z*=conjugado de z)

Z²=Z* --> (A + Bi)²=(A - Bi) --> A² - B² + 2ABi = A - Bi

--> Tenemos 2 ecuaciones:

A=A²-B²

2AB=-B

Despejando B y sustituyendo se obtiene:

raiz(A²-A)(2A+1)=0

Elevando ambos lados al cuadrado:

(A²-A) (2A+1)²=0

--> (A²-A) (4A²+ 4A+1) = 0

Aplicando distributiva:

ECUACION FINAL

4A⁴- 3A²- A = 0

Bien, a simple vista, al tener una ecuacion de grado 4, tendria 4 raices.. Y la solucion seria la opcion D (4 soluciones, osea 4 valores distintos de A y B que cumplan con lo pedido)

Pero quien dijo que no hay alguna raiz doble?

De hecho haciendo unas bajadas por rufini, se encuentra que existe una raiz doble.

Y para verificarlo, la grafica de la funcion f(a)=4A⁴- 3A²- A

es la siguiente:

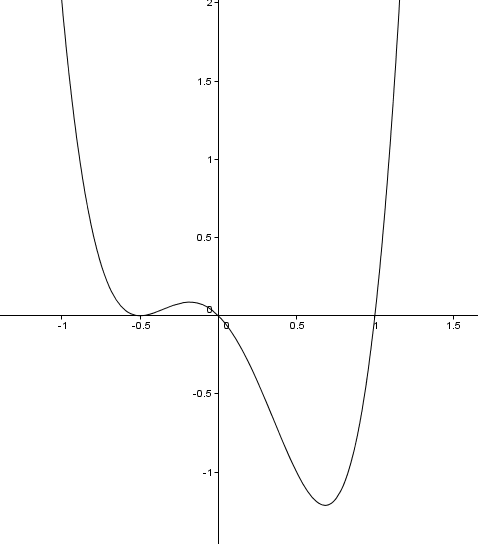
Claramente tiene 2 raices simples y una doble.

Entonces, la opcion correcta cual es? Ninguna de las que estan disponibles.

Me equivoco?

Saludos

Re: Posible error en solucion de julio examen 2012

de Raul Sebastian Castro Scavone - miércoles, 17 de diciembre de 2014, 10:33

Cuando dices

"Tenemos 2 ecuaciones: A=A²-B²y 2AB=-B. Despejando B y sustituyendo se obtiene: raiz(A²-A)(2A+1)=0 ",

te olvidas de B = - raiz(A²-A) (la solución no positiva de B). Esto te cambia la conclusión porque al considerar esta ecuación aparece la solución A = -1/2 y B = - raiz(3)/2 que te falta.

Otro comentario, si tienes la ecuación (A²-A) (2A+1)²=0 no te conviene desarrollar los cuadrados para resolverla, al contrario, lo más sencillo es tener la expresión factorizada como está. O mejor aún, así: A(A - 1)(2A+1)²=0. Entonces las soluciones son A = -1/2, 0 y 1. Sustituyendo en B se obtiene respectivamente: raiz(3)/2, 0 y 0, es decir, las parejas (-1/2, raiz(3)/2), (0,0) y (1,0). Con la ecuación que te olvidaste aparece la cuarta solución.

Saludos,

Sebastián.