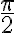Re: Algunos resultados de la semana 11
Hola,
Estuve revisando mis resultados y no llego a lo mismo que vos.
En el primero te cuento un poco cómo me quedaron las cosas, quizás nos demos cuenta qué tenemos distinto.
En cuanto al segundo ejercicio. La parametrización es la misma pero varían los intervalos:
Y el resultado me dio -2/3.
A vos cómo te quedaron esas cuentas?
Saludos.
Florencia
(Editado por Bruno Yemini - sábado, 28 de mayo de 2011, 01:25)
(Editado por Bruno Yemini - sábado, 28 de mayo de 2011, 01:27)
(Editado por Damian Ferraro - sábado, 4 de junio de 2011, 14:57)Re: Algunos resultados de la semana 11
Estuve revisando mis resultados y no llego a lo mismo que vos.
En el primero te cuento un poco cómo me quedaron las cosas, quizás nos demos cuenta qué tenemos distinto.
La parametrización del cilindro:
x= 2^1/2 sn u
y= t
z= 2^1/2 cos u
u (0,2 pi)
p(0,2)
El resultado me quedó -48k pi
En el ejercicio 2 la prametrización es la misma solo que:
u(0,pi/2) (para que x pertenezca al 0,1)
e(0,1)
El resultado me quedó -2/3
Saludos
Florencia
Re: Algunos resultados de la semana 11
Hize todo igual y luego resolvi la integral doble de X(Fiu ^ Fiv) dudv con u y v como vos pusiste
saludos
Re: Algunos resultados de la semana 11
entonces cuando haces X(Fiu^Fiv) te queda raiz de 0
me suena a que esta mal pero no termino de entender que es lo que estoy haciendo mal
ayuda!!
Re: Algunos resultados de la semana 11
Hola? Pido disculpas. La segunda parametrización no es exactamente la misma, es como decís vos. El radio es 1.
Saludos. Voya revisar todas las cuentas de nuevo y vuelvo a poner mis resultados.
Bruno: Muchas gracias por corregir mi post anterior.
Saludos.
Re: Algunos resultados de la semana 11
Re: Algunos resultados de la semana 11
y el uno me dio -48kpi tenia un error en la integral
el ejercicio 3 me dio -2pi
el 4a me dio - pi
el 5 me dio 0 y el 6 tambien
si a alguien le dio distinto les agradezco me lo hagan saber
Re: Algunos resultados de la semana 11
no se como usar el teo de stokes para superficies ¿cual es el borde de el elipsoide??
trate de hacerlo sin el teo pero si uso la parametrizacion
x= raiz 10 cost cos v
y= raiz 10 cost sen v
z= raiz 5 sen t
con t perteneciente (-pi/2,pi/2)
v perteneciente (-pi, pi)
me queda super dificil
ayuda!!
gracias desde ya
Re: Algunos resultados de la semana 11
Otra manera de verlo es separando al elipsoide en dos partes,
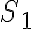 :
: 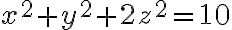 con
con 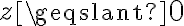 , y
, y 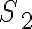 :
: 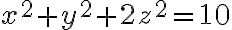 con
con 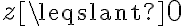 .
.El flujo de
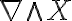 en el elipsoide es la suma de los flujos a través de
en el elipsoide es la suma de los flujos a través de 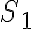 y
y 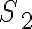 . El teorema de Stokes dice que cada uno de ellos es igual a la circulación de
. El teorema de Stokes dice que cada uno de ellos es igual a la circulación de  en el borde, que para ambos es la misma circunsferencia, pero orientada de dos maneras distintas según se la considere como borde de
en el borde, que para ambos es la misma circunsferencia, pero orientada de dos maneras distintas según se la considere como borde de 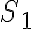 o
o 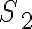 . Sumando todo da que el flujo de
. Sumando todo da que el flujo de 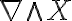 a través del elipsoide da cero.
a través del elipsoide da cero.Con un poco de cuidado esta idea se puede adaptar para demostrar en el caso general lo que decía acerca de las superficies sin borde.
Hola, a mi la parametrizacion del ej 2 me dio:
x=cos u
y=v
z=sen u
u = [pi/2, -pi/2], v= [0,1]
segun nicolas u iria de 0 a pi/2... no entiendo porque
y en cuanto al ej 1 me dio 0
Re: Algunos resultados de la semana 11
(sigo..) sobre el ej 2, si u fuera de 0 a pi/2 estarias tomando la porcion de cilindro tal que z pertenece al [0,1], sin contar la parte de abajo, .. nose si me explico
Re: Algunos resultados de la semana 11
Re: Algunos resultados de la semana 11
Saludos, Andres
Re: Algunos resultados de la semana 11
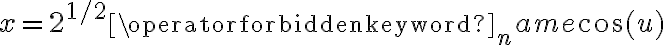
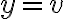

si lo hago asi me queda 48kpi, por que es que se parametriza de la forma que esta arriba?
Gracias
(Editado por Damian Ferraro - jueves, 2 de junio de 2011, 19:16)
(Editado por Damian Ferraro - sábado, 4 de junio de 2011, 12:44)
Re: Algunos resultados de la semana 11
Aclaro, porque me confundí. El párrafo anterior está mal, en el ejercicio 1 de la semana 11 el campo no es perpendicular a la superficie.
Yo parametrice tal cual Gabriel:
x=2 1/2cos u
y=v
z=2 1/2sen u
y no veo porque estaria mal.. de todas formas me dio 0 la integral..

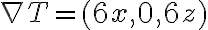
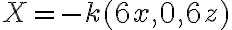
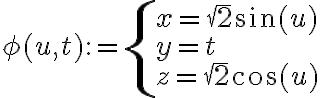
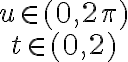
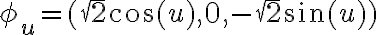
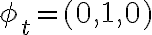
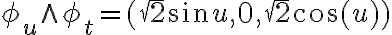
![u\in [-\frac{\pi}{2},\frac{\pi}{2}] u\in [-\frac{\pi}{2},\frac{\pi}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/88f9e69a45675bcccfdb3a2b0de28e9a.gif)
![x=\cos(u)\in [0,1] x=\cos(u)\in [0,1]](https://eva.fing.edu.uy/filter/tex/pix.php/6810861b82112a26d52e03744877ce5b.gif)