El termino que te molesta, el V del lado derecho, que hace que la ecuación no sea homogenea, es constante. Por eso si vas a buscar una solución particular, es conveneniente buscar una solucion constante 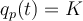 . Esta solución es constante, por lo que su derivada
. Esta solución es constante, por lo que su derivada 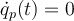 . Como debe satisfacer la ecuación diferencial, queda la ecuación que tu dices.
. Como debe satisfacer la ecuación diferencial, queda la ecuación que tu dices.
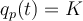 . Esta solución es constante, por lo que su derivada
. Esta solución es constante, por lo que su derivada 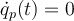 . Como debe satisfacer la ecuación diferencial, queda la ecuación que tu dices.
. Como debe satisfacer la ecuación diferencial, queda la ecuación que tu dices.Por otro lado, qué te parece que sucedería si por ejemplo el potencial no fuera constante, por ejemplo un polinomio en el tiempo t? La idea es que la solución particular que debes buscar es un polinomio en el tiempo, del mismo grado que el polinomio original.
Esa es la idea general, el potencial es constante entonces buscamos soluciones particulares constantes. Espero sirva, saludos, Juan