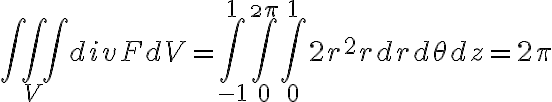buenas, el ejercicio 1 de la versión 2, no da pi? por que según lo que llegué, te queda la 2.integral de x^2+y^2 en V y haciendo el CV a polares y multiplicando por el det. del jacobiano me queda 2.(2pi.(2.ro^4)/4 entre 0 y 1) que es igual a pi no 2pi como marca la solución.
tal vez hice mal algún paso, espero me halla expresado bien.
saludos
para mi pusieron las soluciones al reves... o sea la del 5 es la del 1 la del 4 la del 2 y asi sucesivamente... puede ser esto??
Me parece que esta bien eso que planteas pero la cuenta como vos la escribiste te da 2pi
el 2 que multiplica al ro no iba, perdón, por eso me da pi jeje espero alguien pueda confirmar para estar seguro,
gracias
Yo tambien puse pi, pero me parece que el error esta en que no consideramos la parte de la integral en z, o sea faltaria hacer la integral de pi entre -1 y 1. Eso si da 2pi
se consideró y me dio PI
Estamos en la misma, también lo consideré y me dió pi. También me son vitales esos 8 puntos, veremos..
Aplicando el teorema de Gauss y haciendo cambio de variables 
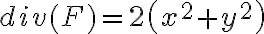
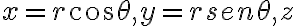
donde ![r\in[0,1]](https://eva.fing.edu.uy/filter/tex/pix.php/62cea0fde53846916db9836dcc1de9c0.png "r\in[0,1]")
, ![\theta\in[0,2\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/e333d87b4a41d9ab978cf70ede38c53a.png "\theta\in[0,2\pi]")
, ![z\in[-1,1]](https://eva.fing.edu.uy/filter/tex/pix.php/6b1bc49b81e059c226f45494834fe172.png "z\in[-1,1]")
tenemos que
