para la parte a) ¿está bien que de esto:
![\[i = \frac{\varepsilon }{{{R_1}}}\]](https://eva.fing.edu.uy/filter/tex/pix.php/fa3109283b8d3abecdaedb6632ffa73f.png "\[i = \frac{\varepsilon }{{{R_1}}}\]")
En la parte c) ¿les da esto:
![\[q(t) = \frac{{{R_2}C\varepsilon }}{{{R_1} + {R_2}}}{e^{\frac{{ - t}}{{{R_2}C}}}}\]](https://eva.fing.edu.uy/filter/tex/pix.php/990bd48201fb320e2d8764aefc1d086a.png "\[q(t) = \frac{{{R_2}C\varepsilon }}{{{R_1} + {R_2}}}{e^{\frac{{ - t}}{{{R_2}C}}}}\]")
Si derivo esta última ec. obtenemos la intesidad, la cual da negativa, ¿cómo se explica eso?
Gracias.
Hola,
para la parte a) ¿está bien que de esto:
En la parte c) ¿les da esto:
Si derivo esta última ec. obtenemos la intesidad, la cual da negativa, ¿cómo se explica eso?
Gracias.
para la parte a) ¿está bien que de esto:
En la parte c) ¿les da esto:
Si derivo esta última ec. obtenemos la intesidad, la cual da negativa, ¿cómo se explica eso?
Gracias.
Federico, hola.
Están bien las dos partes.
Vos elegís un sentido para la corriente y la hallás. Si es negativa, significa que circula en sentido contrario (lo mismo que sucede cuando una velocidad o una fuerza es negativa).
Fijate que vos elegiste una placa del capacitor como +q y luego derivaste hallando una corriente. Ahora, esa corriente, ¿entra o sale de la placa? (adjunto un dibujito). ¡La corriente i2=-i1!
Para pensar cuál es la corriente que obtenés. Imaginate que +q está aumentando. Para eso preciso que la corriente que entra a la placa sea positiva (que "lleguen cargas positivas"), entonces i1 tiene que ser positiva:
Espero que quede más o menos claro. Cualquier cosa preguntá de nuevo o en una clase.
Saludos,
Majo
Están bien las dos partes.
Vos elegís un sentido para la corriente y la hallás. Si es negativa, significa que circula en sentido contrario (lo mismo que sucede cuando una velocidad o una fuerza es negativa).
Fijate que vos elegiste una placa del capacitor como +q y luego derivaste hallando una corriente. Ahora, esa corriente, ¿entra o sale de la placa? (adjunto un dibujito). ¡La corriente i2=-i1!
Para pensar cuál es la corriente que obtenés. Imaginate que +q está aumentando. Para eso preciso que la corriente que entra a la placa sea positiva (que "lleguen cargas positivas"), entonces i1 tiene que ser positiva:
Espero que quede más o menos claro. Cualquier cosa preguntá de nuevo o en una clase.
Saludos,
Majo
En respuesta a Federico Sebastian Diano Benitez
Re: Prá. 5 ej. 4
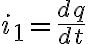
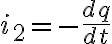
Estimado buenas tardes, aprovecho para comprar resultados, a mi me dio i(t) = (3*epsilon/R*C^2)*(e^t/RC), con las siguientes salvedades R1=2*R2 por eso tal vez haya algun termino diferente al suyo. Igual tengo duda en como tome el sentido de la corriente, entiendo que el Vc(t) en regimen >0 por lo cual si me tomo como sentido la corriente horario pasadno en primera instancia por la placa + y luego por la placa - del capacitor y descargando en la resistencia => la ecuacion es: q/c - R*i =0 pero aca me queda el exponente positivo lo cual me genera dudas, las cuales evacuare mañana en la clase de consulta.
saludos sebastian.-
Xq en la parte A no se tiene en cuenta la otra resistencia?
Cuando recién se cierra la llave, el capacitor está descargado, por lo que VC=0 (¡el potencial en un capacitor es continuo!).
R2 está en paralelo al capacitor, entonces VR=VC=0, y por lo tanto no circula corriente por R2.
Saludos
R2 está en paralelo al capacitor, entonces VR=VC=0, y por lo tanto no circula corriente por R2.
Saludos
Maria Jose buenas tardes, leyendo tu post me voy deoxidando yo en la parte a.- arranque a lo bruto y halle una ecuacion general sin razonar lo que estas comentado lo cual me hubiera ahorrado unos cuantos minutos. Bueno entiendo que igual la deberia haber hallado para la parte b.- entonces obtengo una ecuacion para i2(t) = (epsilon/R)*(e^-3t/RC)) y suponiendo que la operatoria es correcta para tiempos muy grandes entiendo t->infinito por lo cual me queda i2 como una cte. Luego de hallar i2(t) integro y hallo la carga que pasa por el capacitor en regimen. Para tiempos muy grandes tambien me quedaria la carga que tiende a 0 considerando que el capacitor ya tiene su energia maxima. Si esto es correcto me confunde con la parte c.- dado que llego a una ecuacion del tipo dq/dt + q/RC = 0 ahora que condicion inicial utilizo para hallar q(t), seria la q final de la parte b que por mis cuentas seria 0. No se no me convence. Se agradece cualquier ayuda.
gracias y buen fin de semana.
sebastian.-
No sé muy bien a qué le llamás i2, pero en la parte b tampoco es la idea resolver la ecuación diferencial. Fijate que a medida que pasa el tiempo, el capacitor se carga, hasta que llega un momento en que deja de cargarse y la corriente ya no circula por el capacitor, solo por las resistencias. Entonces:
Cuidado que a tiempos grandes la carga en el capacitor NO tiende a 0. Fijate que la carga es q=CV2 (V2 voltaje de la resistencia R2) y si circula corriente por la resistencia entonces V2 no puede valer 0 y por lo tanto hay carga.
Si te quedan más dudas de esto, el lunes y martes hay clases de consulta, capaz es más fácil explicarlo ahí.
Saludos,
Majo.
Cuidado que a tiempos grandes la carga en el capacitor NO tiende a 0. Fijate que la carga es q=CV2 (V2 voltaje de la resistencia R2) y si circula corriente por la resistencia entonces V2 no puede valer 0 y por lo tanto hay carga.
Si te quedan más dudas de esto, el lunes y martes hay clases de consulta, capaz es más fácil explicarlo ahí.
Saludos,
Majo.
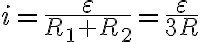
Maria Jose buenas tardes, es evidente que tengo un error de concepto que no me permite avanzar en este ejercicio, si! claro....voy a ir a las clases de consulta para evacuar mis dudas, espero hacerlo entre hoy y ma;ana porque es evidente que algo estoy pasando por alto. Aprovechando la volada te comento que defini como i2 a la corriente que pasa por el capacitor una vez que se cerro S con lo cual me queda i=i1 + i2.
Bueno igual muchas gracias por tu tiempo.
Buen fin de semana para ti y a los foristas.
sebastian.-
Ma. José: cuando se está descargando el capacitor, a priori ¿cómo te das cuenta que signo lleva cada ![\[\Delta V\]](https://eva.fing.edu.uy/filter/tex/pix.php/b6540493f93748d054b25387e03eac85.png "\[\Delta V\]")
?
Gracias
?Gracias
Es un tema de convención. Si vos le asignás +q a una de las placas del capacitor y -q a la otra, entonces
Una cosa es que se puede tomar
al revés, no es lo más cómodo, pero está bien. Ahí quedaría:
Si te queda alguna duda de esto preguntá por acá o en una consulta.
Saludos,
Majo.
Una cosa es que se puede tomar
al revés, no es lo más cómodo, pero está bien. Ahí quedaría:Si te queda alguna duda de esto preguntá por acá o en una consulta.
Saludos,
Majo.
Gracias Majo, ahora si me acaba de andar la neurona! 