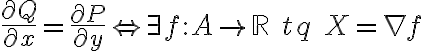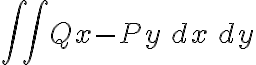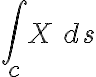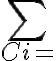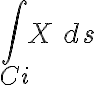Alguien me aclara esto?

Alguien me aclara esto?

de Fernando Gonzalez Hein -
Número de respuestas: 22

Que tengo que fijarme para saber si desde el principio la integral de linea de un campo me va a dar = 0 o no.. ?

Venia bastante bien hasta que me tope con un ejercicio... donde el dominio de X es R-(0,0)

X= ( y/(x^2 + y^2) , x/(X^2 + y^2) )

Segun parece, ese campo integra siempre a 0 en cualquier curva cerrada POR MAS QUE encierre al punto ( 0,0 )

Pero si tomo la parametrizacion (cost,sent) e integro en la cfa de x^2+y^2=1 supuestamente esa integral (que encierra al origen) tendria que dar 2π ...


Si alguien me puede aclarar esto lo amaria con todo mi ser. Gracias


P.D: X es tal cual lo escribi, diferente del ejemplo que damos en clase donde la primera coordenada tiene un (-) delante de la y. Gracias

 

En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Gonzalo Ruben Del Priore Uberti -

Para q la integral de línea sea 0 tenes q integrar en una curva cerrada, además rotor d X =0 y dominio d X simplemente conexo ahí demostramos q es un campo de gradiente y ya ojo q es 0 si es d gradienteen una curva cerrada estoy desde el cel sino se entiende agregarme al face y te digo bien Saludos

En respuesta a Gonzalo Ruben Del Priore Uberti

Re: Alguien me aclara esto?

de Fernando Gonzalez Hein -

No me apareces en face :P

El dominio de X no es simplemente conexo porque el (0,0) no esta incluido en el dominio de X, y si tomo una curva al rededor del (0,0) puede ser la cfa de centro (0.0) cuya integral da 2pi... y no seria de gradientes ? el ejercicio que tomo como referencia dice que es de gradientes y que da 0 la integral en toda curva cerrada.. me marea.

 

En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Pablo Gonnet Banfi -

lo que se me ocurre, que tal vez esté mal, es lo siguiente: si uno tiene A, subconjunto conexo de R2, y define X : A -> R2 entonces vale el teorema:

dQ/dx=dP/dy <---> existe f t.q. X=gradiente de f

(no encuentro el simbolito de gradiente)

AHORA, si yo tengo f : R2\{0,0} ->R y calculo su gradiente, entonces el vector resultante, llamemosle X, ES un campo de gradientes (pese a la particularidad del punto (0,0)), por el simple hecho de que es el gradiente de una funcion

espero haberte aclarado el panorama (y tambien espero que este bien lo que te dije)

saludos

En respuesta a Pablo Gonnet Banfi

Re: Alguien me aclara esto?

de Fernando Gonzalez Hein -

Entonces si tengo ΔX=F (ponele que el Δ sea la funcion gradiente Nabla porque no encuentro la letra) entonces si el dominio del campo X coincide con el dominio de su "potencial" F, e integro en una curva cerrada, puedo asegurar que va a dar 0 independientemente de si tenga agujeros o no en su dominio?

En respuesta a Pablo Gonnet Banfi

Re: Alguien me aclara esto?

de Bruno Yemini -

\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y} \Leftrightarrow \exist f:A \rightarrow \mathbb{R}\ tq\ X = \nabla f

es cierto si A es SIMPLEMENTE conexo. De otra forma es condición necesaria, pero no suficiente para ser de graciente.
En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Fabian Dutra Silva -

Hola, a ver si puedo entender y responder tu duda, que me parece qe ya entendi cual es.

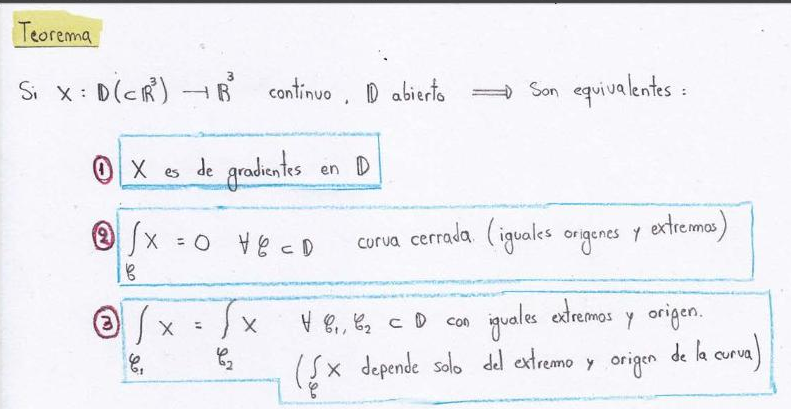
Lo que podés usar para decir "esa integral da cero porque es sobre una curva cerrada" es el teorema que dice: (ver foto)

Por lo tanto, si querés decir que se cumple lo 2, tenés que demostrar que ESTAS EN LAS HIPÓTESIS DEL TEOREMA, y que 1 es verdadera, o 3 es verdadera, aplicas el teorema y podes afirmar lo de la integral igual cero.

La afirmación 3 es más para usarla como 1-3 o 2-3.. porque ponerte a demostrar un PARA TODO no hay chance... no se si hay o no en algún caso pero no importa, la cosa es que en un ejercicio no vas a usar la 3 para demostrar 2.

Por lo tanto solo te queda afirmar 1 para demostrar 2, o sea: UNA POSIBLE respuesta a tu pregunta de como afirmas que una integral da cero sería APLICAR EL TEOREMA DE LA FOTO EN SU VERSIÓN 1-2.

Peeero y acá es donde me parece que le estas errando:

TE ESTÁS OLVIDANDO DE QUE LA DEFINICIÓN DE QUE UN CAMPO SEA O NO DE GRADIENTE DEPENDE DEL DOMINIO.

Esto es lo que te provoca ponele que el mismo campo ese del ejemplo con -y en vez de y sea de gradientes para R2 - Oy y R2 - Ox por separado, pero no para R2 - {0,0}.

Vos cuando decis "Segun parece, ese campo integra siempre a 0 en cualquier curva cerrada POR MAS QUE encierre al punto ( 0,0 )", no se a que te referís exactamente con "encerrar" y tampoco se como demostraste eso.

Pero dejando eso de lado lo que estás diciendo con "Pero si tomo la parametrizacion (cost,sent) e integro en la cfa de x^2+y^2=1 supuestamente esa integral (que encierra al origen) tendria que dar 2π ..." es justamente que ENCONTRASTE UN CONTRAEJEMPLO DE LA PROPOSICIÓN 2 DEL TEOREMA. Es decir: encontraste una integral de ese campo sobre una curva cerrada INCLUIDA EN TU DOMINIO que es distinta de cero. Lo que podes deducir de que esa integral NO te haya dado cero es que X NO ES DE GRADIENTES PARA ESE DOMINIO.

Lo que vos estas haciendo es suponiendo mal que el campo es de gradientes en R2 - {0,0}, y por eso estas llegando erroneamente a la conclusión de que toda integral sobre una curva cerrada da cero, lo que se te contradice con lo que en verdad hiciste bien que fue calcular una integral cerrada incluida en el dominio que te da distinta de cero, y esa contradicción esta haciendo explotar tu balero.

Espero haberte ayudado y que esté bien lo que dije y sino bueno, quedé pegado y que me corrijan los profes. Abrazo

Adjunto subir.png
En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Bruno Yemini -

Hola, ¿por qué decís "según parece, ese campo integra cero en cualquier curva cerrada"?

En respuesta a Bruno Yemini

Re: Alguien me aclara esto?

de Fernando Gonzalez Hein -

Porque en el ejercicio da ese resultado, que en ese campo la integral de linea da 0 para cualquier curva, por mas que rodee al (0,0)..

Me estoy mareando bastante, les dejo adjunto el parcial. Ejercicio 2 del desarrollo, parte 1.

Intento entender todas las explicaciones pero les juro que no logro entender y les pido disculpas, me voy mareando solo. Lo que me esta comiendo la cabeza es: por qué en ese ejercicio de parcial, la integral de linea de cualquier curva cerrada que rodee al agujero da 0.. pero en el ejemplo que damos en clase nos muestran que si el dominio del campo tiene agujeros entonces la integral de linea de una curva cerrada que rodee al agujero no va a dar 0, porque encuentro una curva cerrada rodeando al agujero ( x^2+y^=1 con α(t)=(cost,sent) ) cuya integral de linea da 2π

No se si me explico, o si ya me respondieron y no entendi... De todas formas muchas gracias por responder :)

Saludos !

En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Bruno Yemini -

Fijate que el campo del ejercicio del parcial es distinto al campo que nos diste en el primer mensaje -tenés las coordenadas cambiadas-. El del primer mensaje ni siquiera es irrotacional. Capaz es eso.

Saludos!

En respuesta a Bruno Yemini

Re: Alguien me aclara esto?

de Fernando Gonzalez Hein -

Eso fue un penal y targeta roja..

Pero misma idea, el ejercicio del parcial te pide la integral de linea de un campo irrotacional -pero tiene agujeros- ... si tiene agujeros no afirmabas que no era de gradientes y por tanto la integral de linea no va a dar 0 para toda curva cerrada que rodee la singularidad?

En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Juliana Xavier -

Muchachos:

cito al compañero: 

 

Porque en el ejercicio da ese resultado, que en ese campo la integral de linea da 0 para cualquier curva, por mas que rodee al (0,0).

 

Claramente esto puede pasar, no es ninguna contradicción.  Si agarro una función escalar, definida en un dominio con agujeros, y luego le tomo el gradiente, ese campo integra cero a lo largo de cualquier curva cerrada, independientemente de si rodea agujeros o no.  Este hecho no tiene nada que ver con los agujeros.

 

Los agujeros detectan la falla de que un campo irrotacional sea de gradientes.  Es decir; si tengo un campo irrotacional QUE NO ES DE GRADIENTES, esto se debe a que hay un agujero.

 

Arriba!

En respuesta a Juliana Xavier

Re: Alguien me aclara esto?

de Fernando Gonzalez Hein -

Entonces no puedo afirmar si una integral va a dar 0 o no antes de hacer las cuentas, salvo que el dominio sea simplemente conexo, X de gradientes e integre en una curva cerrada. No lo digo por vago y que no quiera hacer cuentas, solo confundi lo que dicen de "no hacer cuentas si es una curva cerrada y de gradientes" con el tema de los agujeros.. Entonces para concluir, una curva puede dar 0 o no, tenga agujeros o no, tengo que hacer la integral a mano y rezar por que la cuenta no se me vaya a la Luna y listo.

Muchas gracias !! :)

En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Juliana Xavier -

SI EL CAMPO ES DE GRADIENTES LA INTEGRAL SOBRE UNA CURVA CERRADA DA CERO INDEPENDIENTEMENTE DE SI HAY AGUJEROS O NO!!!

En respuesta a Juliana Xavier

Re: Alguien me aclara esto?

de Fernando Gonzalez Hein -

Pero entonces no logro entender por que el ejemplo de la clase shock no es de gradientes, si sus derivadas parciales son iguales, es el "gradiente" de Arctg (y/x), tiene agujeros... y no da cero su integral. Me esta faltando algo para completar mi duda ... lo unico que se me ocurre es: porque el dominio del campo no coincide con el dominio de su potencial. Pero no se, me sigue quedando un vacio en ese tema.

En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Juliana Xavier -

tu función Arctg (y/x) no está definida en el conjunto {x= 0} que es una recta que SEPARA EL PLANO.  cualquier curva cerrada que rodee al agujero CORTA ESTA RECTA, por lo cual no está definida ni siquiera la integral de línea en esa curva, osea que no podés aplicar nada.

 

SE ENTENDIÓ???

En respuesta a Fernando Gonzalez Hein

Re: Alguien me aclara esto?

de Florencia Gomez Villanueva -

Si no podes usar el teorema de las 3 equivalencias entonces si o si tenes q hacer la cuentas. Por lo que veo en este caso no se puede usar porque X no es gradientes porque el dominio de X no es simplemente conexo. Por lo que entendí de todas las explicaciones que dieron... es casualidad que todas integren a 0 .. no tiene nada que ver con los teoremas.... ¿puede ser? Me quedó esa duda

En respuesta a Florencia Gomez Villanueva

Re: Alguien me aclara esto?

de Florencia Gomez Villanueva -

Tu duda es esta?

X NO ES DE GRADIENTES EN ESTE EJEMPLO NO?

SEGUN EL TEO DE LAS 3 EQUIVALENCIAS SI X NO ES DE GRADIENTES... TODAS LAS INTEGRALES DE LINEA SOBRE CURVAS CERRADAS NO SON 0

ENTONCES COMO PUEDEN DAR 0 EN EL EJEMPLO?

 

 

En respuesta a Florencia Gomez Villanueva

Re: Alguien me aclara esto?

de Pablo Gonnet Banfi -

Con el mayor de los respetos a todas las personas que han aportado a este tema, quiero decir que si no escriben de forma correcta, se hace imposible entender las dudas.

Quiero volver un poco, ya que también tengo dudas sobre esto, al principio del asunto, el cual radicaba en que un compañero no entendia la solución del ejercicio. Dicho sea de paso, yo tampoco la entiendo y me gustaria que alguien me despejara de la duda.

La solucion dice en un momento "Sea C la circunferencia de centro en el origen y radio 1. Parametrizandola por (......) un cálculo directo nos muestra que la integal del campo Y en C es igual a cero. Siendo Y irrotacional, esto basta para afirmar que la circulacion de Y a lo largo de cualquier curva cerrada que
encierra al origen es 0."

Y aca es donde mi cerebro explota. Segun lo que acabo de citar textualmente, sabiendo que el campo es irrotacional, el hecho de que la integral del mismo respecto a UNA curva cerrada sea cero implica que la integral respecto a CUALQUIER curva cerrada es cero. Aqui viene mi duda:

¿es esto cierto?

si no lo es, hay 2 posibles conclusiones:

1- yo interpreté mal el enunciado y de ahi el lío que tengo encima

2- la solucion esta mal redactada, por lo que agradecería infinitamente que algun docente la escribiera aqui nuevamente

gracias!

 

En respuesta a Pablo Gonnet Banfi

Re: Alguien me aclara esto?

de Agustin Nicolas Navcevich Costanzo -

Mira a mi tambien me estuvo comiendo la cabeza esto pero después le encontré la vuelta. El tema es así, si te tomas el teorema de Green extendido te dice que la integral de superficie es igual a la integral de línea en una curva menos (dependiendo de la orientación ) la integral en curvas que están dentro de esa, entonces como vos viste q con la cfa te da cero, si te tomas una dentro de ella también va a ser cero ya que si Y es irirotacional entonces la de superficie da cero y al ser igual a las otras dos de línea q una de ellas q te tomas es la cfa entonces caulquiera que te tomes dentro tiene q dar cero para q se cumpla la igualdad, entonces de ahí deducís q  cualquier curva integra cero rodeando a ese punto. No se sí me explique bien pero esa es la idea. ∫∫(Qx-Py)dxdy= ∫F¹ds - ∑∫Fds (Y irrotacional entonces la primer parte cero, tomas ∫F¹ds como la integral de linea en la cfa y da cero por lo tanto la otra parte da cero tambien tomando cualquier curva)