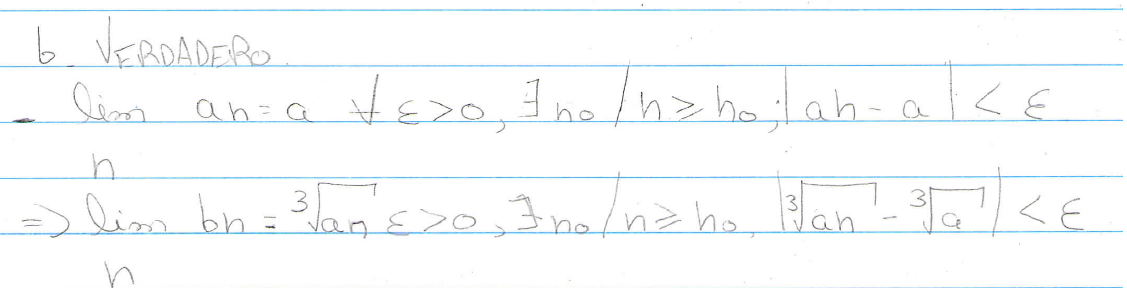Como puedo demostrar esto:
H) $$ \lim_{n\to\infty}a_{n}=a$$
T) $$ \lim_{n\to\infty} \sqrt[3]{a_{n}} = \sqrt[3]{a} $$
Con la definicion de limite
Ahi no hay nada demostrado, solo hay escritas 2 definiciones!!
Algun profe puede decirme si esta bien este razonamiento?
De la hipotesis obtengo: (Por definicion de límite)
$$|a_{n}-a|< \xi _{1}$$
Eso tambien se puede escribir (Si no me equivoco) como:
$$a- \xi _{1} \le a_{n} \le a+ \xi _{1}$$
Entonces teniendo esto, empezamos: elevando cada lado de la igualdad a la 1/3 (poniendo raiz tercera)
$$ \sqrt[3]{a- \xi _{1}} \le \sqrt[3]{a_{n}} \le \sqrt[3]{a+ \xi _{1}} $$
A su vez, usando este clase de propiedad:
$$ \sqrt[3]{c+b} \le \sqrt[3]{c} + \sqrt[3]{b} $$
y
$$ \sqrt[3]{c-b} \le \sqrt[3]{c} - \sqrt[3]{b} $$
Puedo aplicarlas y deduzco:
$$ \sqrt[3]{a} - \sqrt[3]{ \xi _{1}} \le \sqrt[3]{a_{n}} \le \sqrt[3]{a} + \sqrt[3]{ \xi _{1}} $$
Que usando lo que escribi de rojo, me queda igual a:
|$$ \sqrt[3]{a_{n}} - \sqrt[3]{a}| < \sqrt[3]{ \xi _{1}} $$
Tomamos $$ \xi = \sqrt[3]{ \xi _{1}} $$
Y se cumple la definicion del limite que esta en la tesis, osea, se cumple la tesis.
¿Esta bien? Perdon que joda con esta demostracion que seguro es una papa para los demas. El tema es que no he entrado a los practicos y ta tuve que recurrir a acá para verificar.
Hola, no se a los demás a mi tampoco me resulta una papa, hace días que vengo pensando en algo como lo que hiciste, creo que por ahí va, sin embargo tengo mis dudas porque en el último paso en la doble desigualdad sustituiste por algo mayor según la propiedad que usaste. Es decir llegaste a que a<b<c si encontras algo un d<a entonces podes asegurar que d<a<b<c entonces d<b<c pero en este caso el d es d>a con lo cual no se puede asegurar que que d siga siendo <b. Que opinas?
Re: Demostracion
Se me ocurrió una.
Si no te convence espero que algún profe se apiade de nosotros. Saludos.
Si ya vi, pero enrealidad es un error de tipeo. Lo que quise poner fue esto:![]()
Que si fuese cierto, la demostracion estaria bien. El problema es que estuve viendo y acabo de ver que eso solo se cumple si c es mayor que b.
Conrespecto a tu demostracion: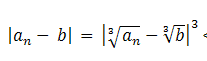
Esta igualdad que escribiste, es erronea. Podes verificarlo dando valores a las variables.
Tampoco entendi esta parte: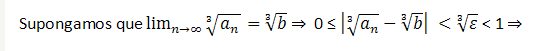
Porque tomas el epsilon menor que 1? El epsilon es arbitrario y depende de n0. Nose si es conveniente acotarlo, tampoco se si esta permitido.
Esta demostracion no creo que sea por absurdo, porque deberias probar que no se cumple para cualquier numero real distinto de raiz tercera de (an) Cosa que no podes ya que hay una infinidad de numeros distintos a ese.
Vamos por partes.
El epsilon es arbitrario estamos de acuerdo, por lo tanto lo podes tomar entre 0 y 1, que ademas es donde es interesante tomarlo y la definición cobra sentido, ahora nota por ejemplo que la raíz cúbica de 1/1000 es 1/10 dicho de otra forma como los números que se comparan están entre 0 y 1 la raíz cúbica (y en general la raíz enésmia) de un número a es mayor que el propio número. Me equivoque también donde dice igual debe decir menor o igual, si te fijas le puse un asterisco a esa afirmación que al final trato de explicar haciendo las cuentas, te queda el desarrollo del binomio al cubo donde sustituyo la raíz cúbica de an por su limite y hay dos términos que se cancelan quedando el igual, que es erróneo porque el igual se da sólo si la sucesión toma el valor del límite.
Por último toda esta perolata lleva a que an tiene límite "b" que necesariamente debe ser igual a "a" de lo contrario tendrías una sucesión con dos límites distintos para n susficientemente grande lo cual es absurdo por la unicidad del límite.
Buenas. Como pusieron por ahí, vamos por partes:
1) Como bien dijo Luciano, la primer demostración que tiraron por ahí falla ya que NO es cierta la propiedad:
$$\sqrt[3]{c-b} \geq \sqrt[3]{c}-\sqrt[3]{b}$$
2) La segunda demostración tampoco es correcta, por 2 motivos: el primero, que la igualdad $$|a_n-b|=|\sqrt[3]{a_n}-\sqrt[3]{b}|^3$$ no es correcta. El segundo es que, aunque dicha igualdad fuese correcta, el razonamiento por absurdo requiere negar la tesis, que no es lo que se planteó. Negar la tesis implicaría decir "$$\sqrt[3]{a_n}$$ no tiende a $$\sqrt[3]{a}$$", que no es lo mismo que decir "$$\sqrt[3]{a_n}$$ tiende a la raíz cúbica de otro número real" (b en este caso).
3)Finalmente para demostrar este ejercicio, tal vez les sea de utilidad la igualdad:
$$c-d=\frac{c^3-d^3}{c^2+cd+d^2}$$
o, llamando $$c = \sqrt[3]{x}$$ y $$d= \sqrt[3]{y}$$:
$$\sqrt[3]{x}-\sqrt[3]{y}=\frac{x-y}{x^{2/3}+\sqrt[3]{xy}+y^{2/3}}$$
Espero que les sea de ayuda.
Saludos
Bueno a ver que les parece esta:
Tenemos por hipotesis:![]()
A partir de aca separamos en 2 posibilidades:
La primera:
$$a_{n} \ge a$$
Suponiendo eso, puedo quitar las barras del valor absoluto:
$$a_{n}-a< \xi _{1}$$
Elevamos a 1/3 ambos lados:
$$ \sqrt[3]{(a_{n}-a)} < \sqrt[3]{ \xi _{1}} $$
Esta propiedad si se cumple cuando $$c>b$$ (Esto lo deduje con unas simples cuentas, que me corrija el profesor si me equivoco)![]()
Sustituyo an=c y a=b:
$$ \sqrt[3]{a_{n}} - \sqrt[3]{a} < \sqrt[3]{(a_{n}-a)} < \sqrt[3]{ \xi _{1}} $$
Por transitividad:
$$ \sqrt[3]{a_{n}} - \sqrt[3]{a} < \sqrt[3]{ \xi _{1}} $$
Como
$$ \sqrt[3]{a_{n}} \ge \sqrt[3]{a} $$
Puedo agregar las barras de valor absoluto nuevamente y obtengo:![]()
Lo que verifica la tesis. Y queda demostrado.
Ahora viene la parte que se complica un poquito mas.
La segunda posibilidad:
Y es suponiendo $$a_{n}<a$$
Tenemos:![]()
Quito las barras. (Adecuadamente, esta vez multiplicando por (-1) ya que $$a_{n}<a$$)
$$a-a_{n}< \xi _{1}$$
Elevo a la 1/3 ambos:
$$ \sqrt[3]{a-a_{n}} < \sqrt[3]{ \xi _{1}} _{}$$
Uso la misma propiedad de hoy, en este caso sustituyo a=c y an=b
$$ \sqrt[3]{a} - \sqrt[3]{a_{n}} < \sqrt[3]{ \xi _{1}} $$
(Aca hice la transitividad directamente sin escribirla, pero es lo mismo que hice en el caso 1)
Como $$a_{n}<a$$
$$ \sqrt[3]{a} > \sqrt[3]{a_{n}} $$
Lo que me permite agregar las barras de valor absoluto nuevamente: (Discuplen mis barras de valor absoluto deformes, es que no se hacerlas con la herramienta de moodle)
|$$ \sqrt[3]{a} - \sqrt[3]{a_{n}} $$| $$< \sqrt[3]{ \xi _{1}} $$
|$$ \sqrt[3]{a} - \sqrt[3]{a_{n}} $$| = ![]()
Asi que:![]()
Tomamos $$ \xi = \sqrt[3]{ \xi _{1}} $$
Y se verifica la tesis.
Es decir, para ambos casos se verifica la tesis. Asi que queda demostrado..
Es masomenos lo que hice hoy, pero mucho mas firme el razonamiento.
Respecto a las 2 igualdades que recomendo Bernardo, no supe usarlas. Lo intente. Pero no les encontre lugar.