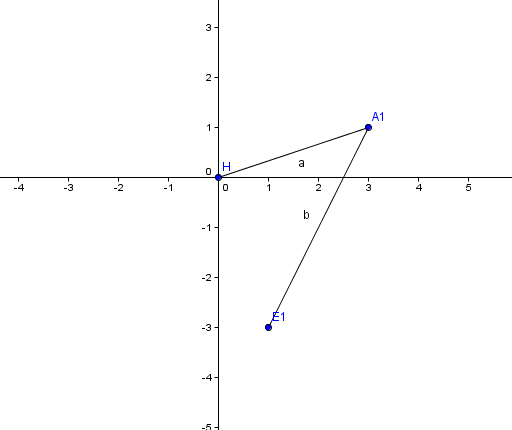
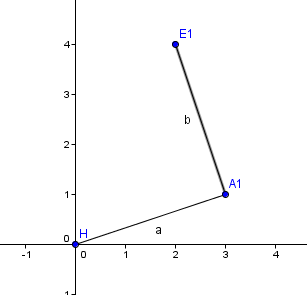
Intente resolverlo por metrica y no pude. Se que la idea es usar complejos pero todavia no los domino muy bien.
Termine consultando butenzar.com y supuestamente esta es la solucion: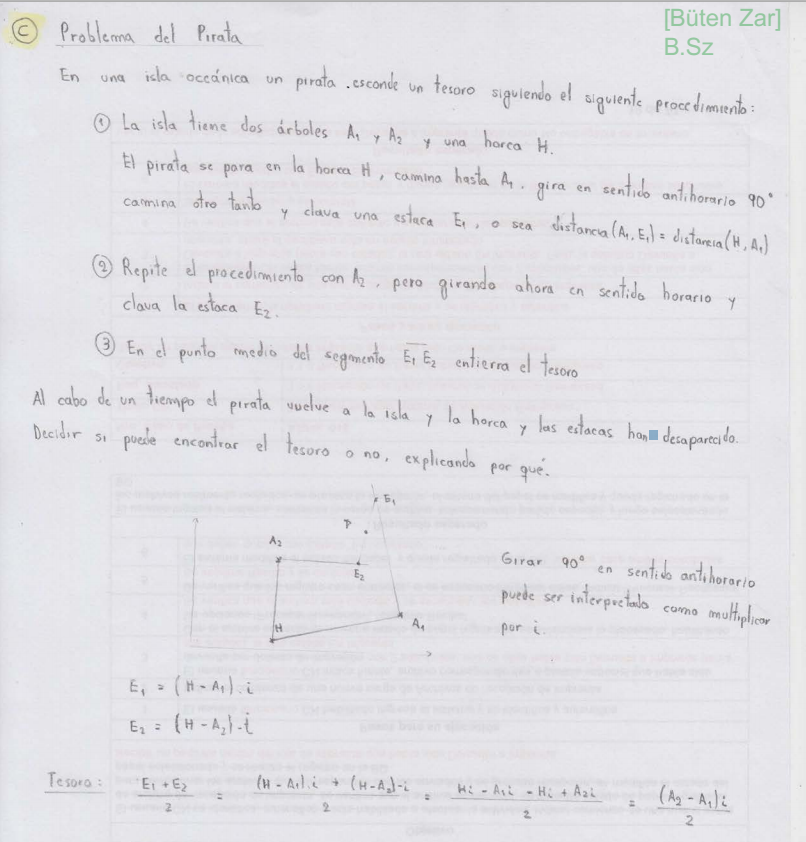
Pero no me cierra, cuando escribe que:
E1= (H - A1) (i)
Cuando trato de llevarlo a los ejes, y le doy valores cualqueira a las coordenadas de H, y A1, uso esa "formula" y obtengo un punto, que no forma 90 grados y ni si quiera dista lo mismo de H que A1. Como dice la letra.
Esta mal esa solucion, o yo ando tan mal para este tema que ni si quiera me sale una multiplicacion de complejos?