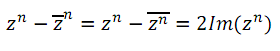Primero tomás $$ (1+i)^{n} $$ como $$ z^{n} $$ y lo mismo con el otro término, entonces tenés $$ z^{n} $$ menos el conjugado también elevado a n.
Ahora escribís los dos números en notación polar, el módulo es el mismo: $$ \sqrt [2] {2} $$. Y el argumento es pi/4 para 1+i y -pi/4 para 1-i.
Y sabemos que elevar un complejo a la n es elevar el módulo a la n y multiplicar el argumento por n. Entonces $$ z^{n} = \sqrt [2] {2} ^{n} e^ {\frac {i*n*pi}{4}} $$ y el de 1-i es igual pero con el argumento negativo.
Restamos:
$$ (1+i)^{n} - (1-i)^{n} = (\sqrt [2] {2}) ^{n} e^{ \frac {i*n*pi}{4} } $$ - $$ (\sqrt [2] {2}) ^{n} e^{ \frac {-i*n*pi}{4} } $$
Se saca el módulo de factor común y nos queda algo similar a la función seno compleja, pero nos falta que sea sobre 2i:
$$ (1+i)^{n} - (1-i)^{n} = (\sqrt [2] {2}) ^{n} (e^{ \frac {i*n*pi}{4} } $$ - $$ e^{ \frac {-i*n*pi}{4} }) $$
Entonces vamos a transformar ese paréntesis con los e en $$ sen(\frac {n*pi}{4}) $$, y dejamos el 2i del denominador afuera multiplicando al módulo:
$$ (1+i)^{n} - (1-i)^{n} = 2i (\sqrt [2] {2}) ^{n} sen(\frac {n*pi}{4}) $$
Pero $$ sen(\frac {n*pi}{4}) $$ toma distintos valores según n, entonces ahí probas vos, cuantos valores distintos podés tomar hasta que se repitan los resultados, y ta. Tenés tu resta de complejos elevados a la n, en distintos casos :)
(No tenés idea lo que me costó escribir esto con las fórmulas, me llevo un premio)

 + 2pi = 47pi/36
+ 2pi = 47pi/36