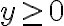Buenas,
no le encuetro vuelta a esto,
Dado el campo X: R2 --> R2
Se sabe que es irrotacional y que X(t,0)=(2t+1,1) y la curva {(x,y) R2/ x^2+y^2=1 con y>=1} recorrida antihorario.
El tema puntual es que no logro sacar la segunda componente del campo es decir si tenemos X(x,0)=(2x+1,1)
como saco X(x,y)?
ya lo intenté integrando las derivadas opuestas que da el rotor(Rot(X)=Qx-Py=0), pero no hay caso, agradezco la ayuda, abrazo
Para resolver el ejercicio no necesitás ese dato -y creo no lo podrías obtener con los datos del problema-, ¿qué propiedades conocés de los campos irrotacionales?
Y la curva es con 
, no 1. Eso es importante.
Abrazo
tenés razón, me equivoqué con el y>=1
lo saqué por medio de f(-1,0)-f(1,0) (diferencia de potenciales escalares)
Ahora bien, tengo otra duda en el ejercicio 1 del segundo parcial 2013
no era que el flujo de todo campo solenoidal a traves de una sup cerrada es cero?
lo rebusqué por medio de stokes igual
x solenoidal existe Y=ROT(F)
∫ ∫F= ∫ ∫ROT(F)= ∫Y
y en la última igualdad apliqué stokes
la verdad q no se como seguir
mala mía gente, no me había dado cuenta q era en las paredes del cilindro je
ahí va, saludos.