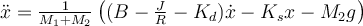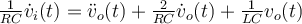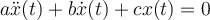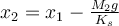Consultas

Buenas. No me queda claro qué es la entrada y qué es la salida en este ejercicio. Llegué a la ecuación diferencial :

$\ddot x = \frac{1}{M_1+M_2} \left( (B-\frac{J}{R}-K_d) \dot x -K_sx -M_2g \right)$

Si no le pifié a ninguna cuenta. Ahí sólo está la posición, que asumo es la salida. ¿Cuál sería la entrada, la velocidad angular? No tiene mucho sentido, porque te quedaría simplemente 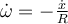 $\dot \omega = - \frac{\dot x}{R}$ ¿No?

Tampoco me queda claro qué quieren decir con que la ecuación homogénea sea igual a la del ejercicio anterior. La ecuacion diferencial del ejercicio anterior me quedó :

$\frac{1}{RC} \dot v_i(t) = \ddot v_o(t) +\frac{2}{RC}\dot v_o(t) +\frac{1}{LC}v_o(t)$

Supongo que por homogénea quiere decir que v_i(t) vale cero, o sea que debería ser una ecuación del estilo:

$a \ddot x(t) + b \dot x(t) + c x(t) = 0$

En este caso, no importa el tema de si hay o no, y cuál es la entrada, porque no aparece. Si la gravedad actúa sobre el sistema (cosa que no está especificada en la letra, pero por el dibujo asumí que si), no se puede escribir una ecuación así. Si la gravedad no actúa, si se puede. Otra cosa que vi (revisando mensajes del foro viejo) es que la constante B, es un coeficiente de viscosidad (o sea, que la fuerza es 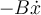$- B \dot x$ ), y la letra da a entender que es un coeficiente de rozamiento.