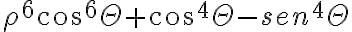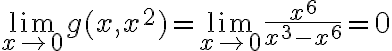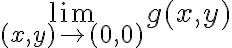Ejercicio de continuidad, 2S - 2020

Ejercicio de continuidad, 2S - 2020

de Mateo Roman Allonca Maldonado -
Número de respuestas: 2

Hola, tengo una duda de este ejercicio. La letra dice lo siguiente:

image.png

en g(x,y) si nos aproximamos por 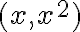(x,x^2) nos queda: 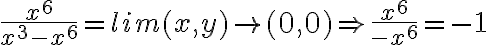\frac{x^6}{x^3-x^6} = lim (x,y) \rightarrow (0,0) \Rightarrow \frac{x^6}{-x^6} =-1 , por lo tanto no existe el limite de g(x,y)

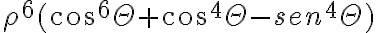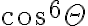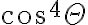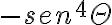Me queda la duda en f(x,y). Si tomo polares me queda: \rho^6(cos^6 \Theta+cos^4 \Theta-sen^4 \Theta) la última parte no es acotada, no? Porque si theta se mueve desde 0 a 2 pi, cos^6 \Theta , cos^4 \Theta y -sen^4 \Theta siempre van a tomar valores diferentes. Es decir que el límite no existe, es correcto este planteo? Aguardo respuesta, gracias. 
En respuesta a Mateo Roman Allonca Maldonado

Re: Ejercicio de continuidad, 2S - 2020

de Mateo Roman Allonca Maldonado -
Ahora que me doy cuenta, queda \rho^6cos^6 \Theta+cos^4 \Theta-sen^4 \Theta Que tiene más sentido que lo anterior. 
En respuesta a Mateo Roman Allonca Maldonado

Re: Ejercicio de continuidad, 2S - 2020

de Florencia Cubria -

Hola Mateo, tienes un error de cálculo en el siguiente límite:

\lim_{x\to 0} g(x,x^2)=\lim_{x\to 0} \frac{x^6}{x^3-x^6}=0

Deberías demostrar que ese \lim_{(x,y)\to (0,0)} g(x,y) no existe pero de otra forma.

Para la función f te recomiendo que te acerques al punto (0,0) por las rectas de los ejes coordenados.

Dime si algo no se entendió.

Saludos, Florencia.