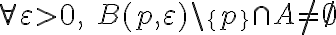Foro de Ejercicios fuera de los Prácticos

Hola, quería saber si mi razonamiento está correcto. La letra dice lo siguiente:

Comencemos por (I), Entiendo que A no es abierto ya que 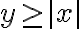$y \geq |x|$ . Es decir, no todos los puntos del conjunto A son interiores. 

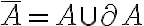
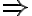
Luego en (II) nos piden verificar si la clausura de A es igual al conjunto en si mismo. Por definición sabemos que 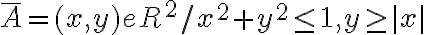$\overline{A} = A \cup \partial A$ $\Rightarrow$ $\overline{A} = {(x,y) e R^2/ x^2+y^2 \leq1, y \geq |x| }$ . Por lo tanto la segunda afirmación es falsa.

En (III) podemos verificar que (0, 1/2) es un punto de acumulación de A si es un punto interior del conjunto, (esto es por definición). Como el punto es interior de A, entonces la afirmación es verdadera. 

El razonamiento deducido es correcto? Hay algún error? Aguardo respuestas, gracias.