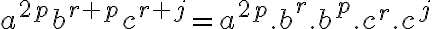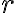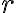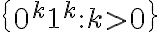[2023][1er Parcial][Ejercicio 2][Parte b]

[2023][1er Parcial][Ejercicio 2][Parte b]

de Luca Scaboni Morales -
Número de respuestas: 2

Buenas tardes, realizando este ejercicio yo llegué a la conclusión de que es falsa la afirmacion, sin embargo, en la solucion dice que es verdadera. Mi razonamiento fué separar en casos para cuando p = 1 y cuando p = 2, obtener una expresion regular r1 y r2 para ambos casos y luego colocarlas como (r1 | r2), de modo que es una expresion regular para el lenguaje.

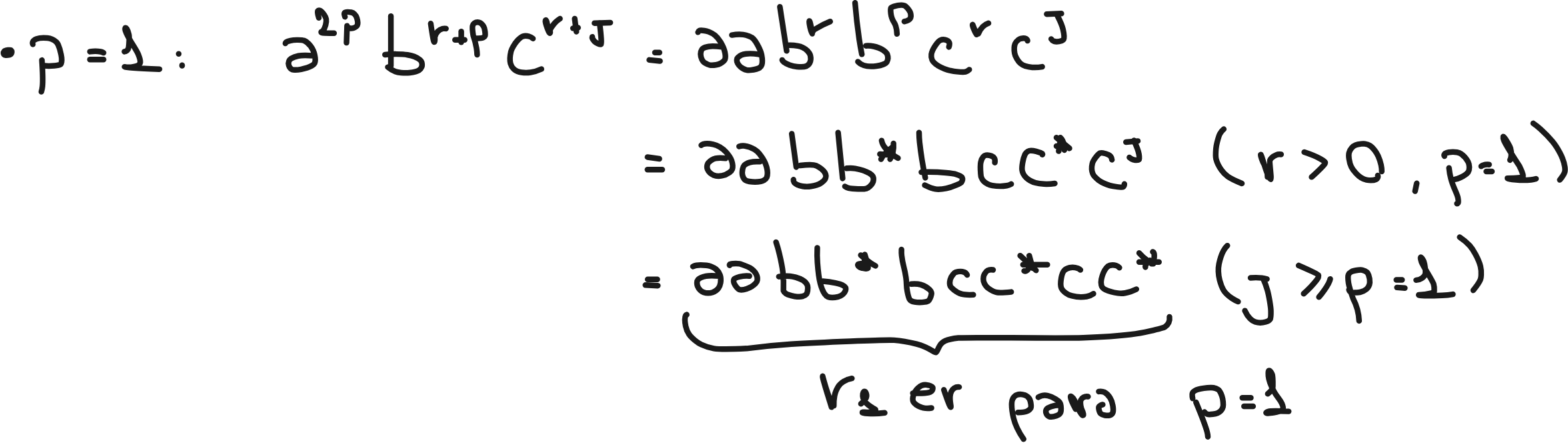
image.png

En la imagen se puede observar este razonamiento, como r no está acotada, solo es mayor a 0, es colocar el caracter seguido de el propio caracter*, al separar en casos, si p = 1 o p =2 se conoce la cantidad de a's, y luego, como j >= p, conociendo el valor de p puedo simplemente colocar la cantidad necesaria para superar esa cantidad y despues el caracter*.

En respuesta a Luca Scaboni Morales

Re: [2023][1er Parcial][Ejercicio 2][Parte b]

de Santiago Gongora -

Buenas tardes, Luca.
El asunto con este lenguaje es que no es regular porque hay una dependencia entre las b's y las c's:

a^{2p} b^{r+p}c^{r+j} = a^{2p}.b^r.b^p.c^r.c^j

Para que una tira pertenecezca al lenguaje, hay una cantidad de b's tiene que ser r y hay una cantidad de c's que también tiene que ser r . Como bien decís, r no está acotado. Por lo tanto, no hay forma que se pueda, de antemano, saber cuáles son los valores que puede tomar y, por lo tanto, estamos ante un caso similar a la dependencia que hay en el famoso \{0^k 1^k: k>0 \} que Juanjo muestra en el teórico (que no es regular).

Así que como hay una dependencia entre las b's y las c's que no puede ser modelada con una expresión regular, entonces el lenguaje no es regular, y hay que probarlo con el contrarrecíproco del Pumping Lemma. 

Espero que haya quedado claro y, si no, a las órdenes.
Santi
En respuesta a Santiago Gongora

Re: [2023][1er Parcial][Ejercicio 2][Parte b]

de Diego Garat -
hola:

agrego a lo que dice santiago:

a pesar del r en común, si j y p tomasen cualquier valor, se "rompería" la relación entre la cantidad de bes y ces y el lenguaje sería regular. pero observa que j y p sí están relacionados, j es al menos p (j>=p) según la definición del lenguaje, con lo que la cantidad de ces es siempre _al menos_ la cantidad de bes (r+p<=r+j). esa relación no la podés controlar con una cantidad finita de estados.

en particular, este ejercicio agrega que p toma únicamente dos valores, pero eso no cambia la desigualdad. retomo tu caso para p=1: las tiras tienen la forma  aa.b^(r+1).c^r(r+j)  con j>=1, r>0. observá que j>=1, luego (r+1)<= (r+j)

la tira. x=aa.bbb.cc pertenece a L(aa.bb*b.cc*cc*) = L(aa.bbb*.ccc*), pero x no pertenece a L2, pues no se cumple:
3 = |x|b <= |x|c =2.

saludos,
d.-