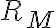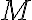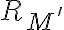Buenas tardes,
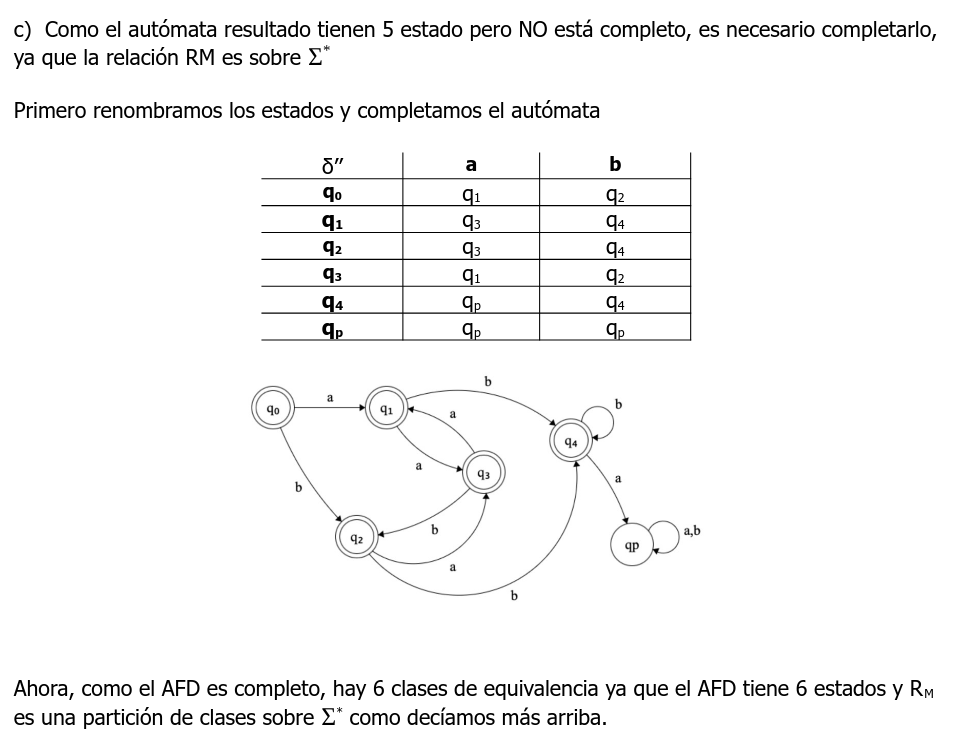
Teniamos la duda ya que en la solucion se plantea que el automata tiene 6 clases, pero nosotros, luego de agregar el pozo, llegamos a que habian 2 clases (la clase de los finales y la clase del pozo).
Luego intentamos minimizarlo, llegando a 4 clases ([p0,p3],[p1,p2],[p4],[pp]), pero no llegamos a las 6 clases mencionadas en la solucion.
adjunto imagen de la solucion del parcial.