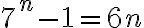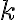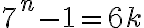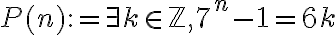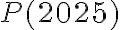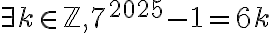Ejercicio 7 - práctico 1 duda existencial

Ejercicio 7 - práctico 1 duda existencial

de Mateo Roman Allonca Maldonado -
Número de respuestas: 2

Hola, buenas tardes a todos. Resulta que tengo una duda con este ejercicio. la letra dice lo siguiente:

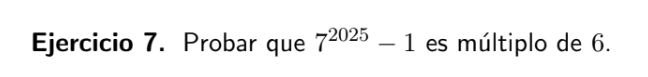
image.png

En clase se dió que se puede resolver simplificando a 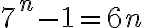7^n - 1 = 6n . Para practicar para el parcial, quise resolverlo tal cual como está en la letra. Entonces, resumiendo brevemente todos los pasos y deduciendo que el paso base es cierto, se parte de 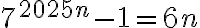7^{2025n} - 1 = 6n (hipótesis inductiva) y se quiere demostrar que se cumple p(n+1)= 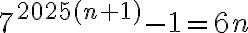7^{2025(n+1)} - 1 = 6n (tesis inductiva)

Entonces al hacer un poco de cuentas, nos queda que p(n+1)= 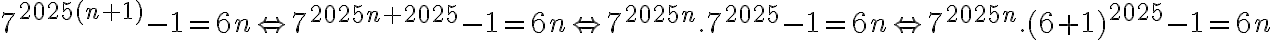7^{2025(n+1)} - 1 = 6n \Leftrightarrow 7^{2025n+2025} - 1 = 6n \Leftrightarrow 7^{2025n}.7^{2025} - 1 = 6n \Leftrightarrow 7^{2025n}.(6+1)^{2025} - 1 = 6n

Ahora viene el problema, resulta que si queremos hacer el binomio de newton para 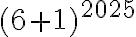(6+1)^{2025} son mas de 1700 dígitos. Entonces, ¿cómo puedo despejar este numero de tal manera que me quede de alguna forma la hipótesis inductiva ( 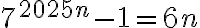7^{2025n} - 1 = 6n   )y un múltiplo de 6? Cosa que por propiedad de suma de multiplos, de 6n

Saludos. 
En respuesta a Mateo Roman Allonca Maldonado

Re: Ejercicio 7 - práctico 1 duda existencial

de Gabriel Mello -
Hola Mateo.

Tenés un problema grave que en el mejor de los casos es falta de atención al detalle y en el peor una confusión profunda sobre lo que escribiste.

Lo primero es que es falso que 7^n -1 = 6n salvo cuando n vale 0 o 1. Lo que seguramente se dijo en clase y que no es simplificar si no simplemente la definición de ser múltiplo es que basta probar que para todo n existe un entero k \textbf{que depende de n} para el cual se cumple que 7^n -1 = 6k .

En lo siguiente voy a suponer que esto fue sólo una falta de atención y que lo que quisiste poner fue eso.

La proposición a la cual se le aplica el principio de inducción pasa a ser entonces P(n) := \exists k \in \mathbb{Z}, 7^n -1 = 6k por lo que en la prueba por inducción de que esta propiedad es cierta para todos los naturales no aparece ningún 2025 ni ningún binomio de newton. Lo que se hace es probar que la propiedad es cierta para todo natural y como en particular 2025 es un número natural se cumple P(2025) . Esto es: \exists k \in \mathbb{Z}, 7^{2025} -1 = 6k .

Saludos,
Gabriel