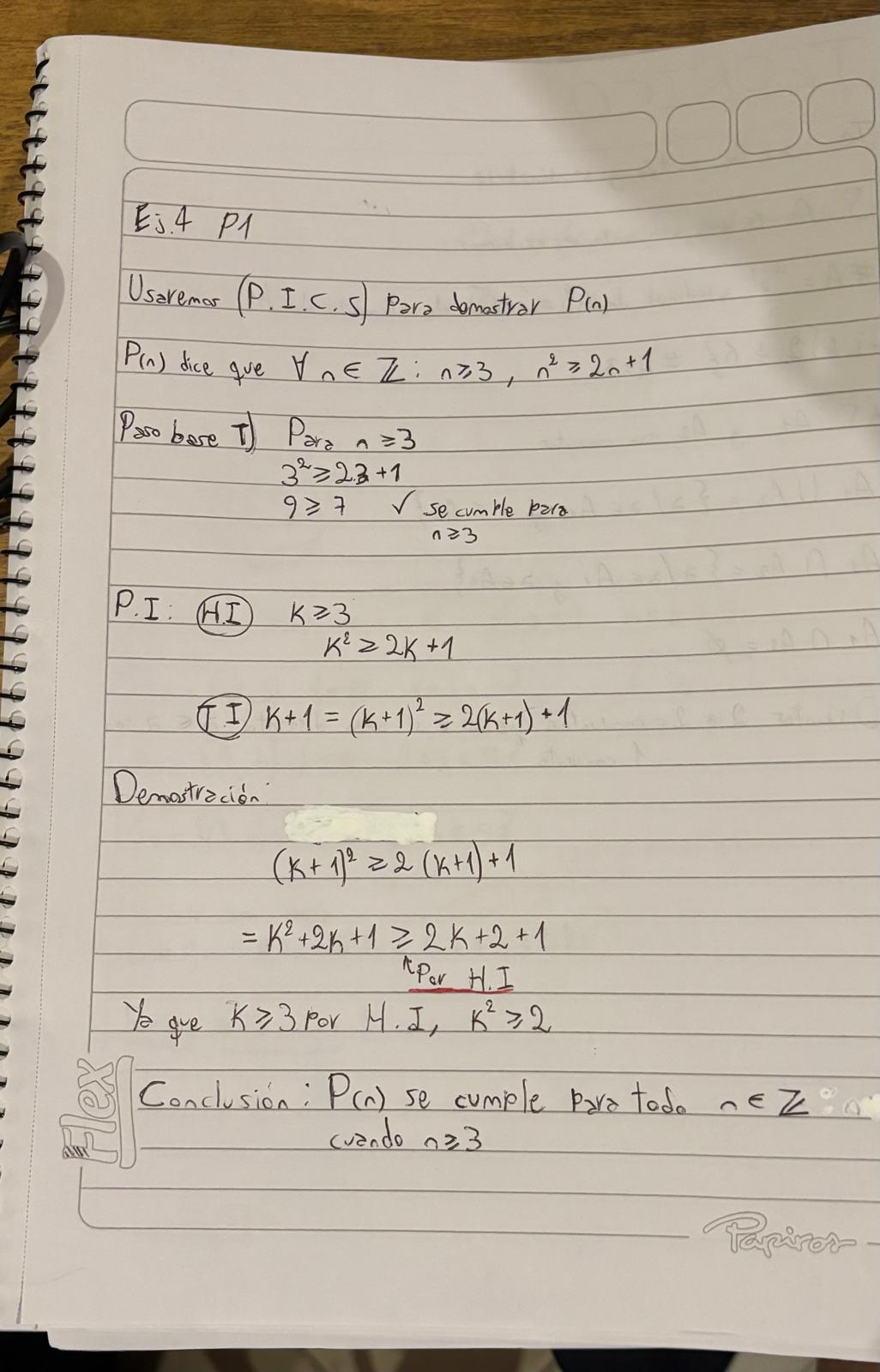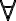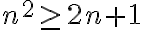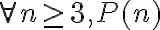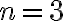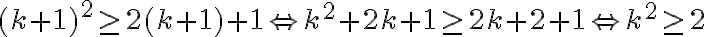Me gustaría saber si mi resolución del ejercicio está bien.
Usaremos (P.I.C.S) Para demostrar P(n)
P(n) dice que para todo n Entero tal que n ≥ 3, n² ≥ 2n+1
Paso Base:
Para n ≥ 3
3² ≥ 2*3+1
9 ≥ 7
se cumple para n ≥ 3
Paso Inductivo:
H.I:
K ≥ 3
K² ≥ 2K+1
T.I:
K+1= (K+1)² ≥ 2(K+1)+1
Demostración:
(K+ 1)² ≥ 2(K+1) +1
= K²+2k+1 ≥ (Por H.I) 2K+2+1
Ya que K ≥ 3 por H.I, K² ≥ 2
Conclusión: P(n) se cumple para todo n Entero cuando n ≥ 3