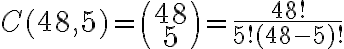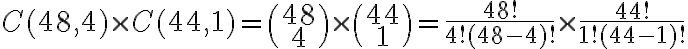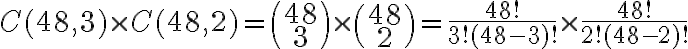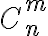Ejercicio 11 práctico 2

Ejercicio 11 práctico 2

de Mateo Roman Allonca Maldonado -
Número de respuestas: 1

Hola, en este ejercicio me gustaría que me digan si está correcto el razonamiento. La letra es la siguiente: 

image.png

a) Para la parte a, lo que pensé es ¿De cuantas formas se pueden sacar 5 cartas del mismo palo de un mazo? Entonces sería una combinación de 48 en 5. 

C(48,5) = \binom{48}{5} = \frac{48!}{5!(48-5)!}

b) En b, la cosa cambia un poco. ¿De cuantas formas posibles puedo sacar cuatro ases de 48 cartas? Además, faltaría una restante que es al azar del mazo. Entonces es una combinación de 48 cartas en 4 por una combinación de 44 cartas en 1 

C(48,4) \times C(44,1) = \binom{48}{4} \times \binom{44}{1} = \frac{48!}{4!(48-4)!} \times \frac{44!}{1!(44-1)!}

c) En esta parte, es el mismo razonamiento de la parte b. ¿De cuantas formas posibles puedo sacar 4 cartas del mismo valor de un mazo de 48 cartas? Y además, la restante que sea al azar. Entonces es:

C(48,4) \times C(44,1) = \binom{48}{4} \times \binom{44}{1} = \frac{48!}{4!(48-4)!} \times \frac{44!}{1!(44-1)!}

d) Aquí debemos elegir 3 ases entre 48 cartas y luego 2 sotas del mazo restante. Es una combinación de 48 en 3 por una combinación de 45 en 2. 

C(48,3) \times C(48,2) = \binom{48}{3} \times \binom{48}{2} = \frac{48!}{3!(48-3)!} \times \frac{48!}{2!(48-2)!}

e) Idem parte d. Un par está conformado por dos cartas iguales, entonces se necesita hacer una combinación de 48 en 3 para saber cuales son las posibilidades de obtener 3 ases en una mano y luego multiplicarlo por una combinación de 45 en 2. Que sería el mazo restante por el par. 

¿Es correcto el razonamiento? Saludos.
En respuesta a Mateo Roman Allonca Maldonado

Re: Ejercicio 11 práctico 2

de Pablo Romero -
Buenas tardes Mateo:
Ten presente que las combinaciones de m en n, que denotamos mediante el símbolo C_{n}^{m}, es igual a la cantidad de subconjuntos de n elementos dentro de un conjunto de m elementos.

Teniendo en cuenta dicha definición, resolvamos la parte (a). Para determinar la cantidad de maneras de obtener 5 cartas del mismo palo, lo que podemos hacer es poner, primero, 4 pilas de 12 cartas cada una, donde una pila tiene bastos, otra pila tiene copas, otra tiene oros, y otra tiene espadas.

Para proceder a elegir 5 cartas del mismo palo, conviene observar que debemos realizar 2 tareas de forma independiente:
(1) Elegir una de las 4 pilas, y luego
(2) Elegir 5 cartas cualesquiera dentro de dicha pila previamente seleccionada (que tiene 12 cartas)

Notar que, por la regla del producto, el resultado se va a obtener tras multiplicar la cantidad de maneras de realizar la tarea 1 y la cantidad de maneras de realizar la tarea 2.
Dejo que completes la parte (a) y que revises las partes restantes, que no están bien.

Cordiales saludos,
Pablo.